簡介
用來計算狹義的貨幣乘數。在基礎貨幣一定的條件下,貨幣乘數與貨幣供給成正比。銀行存款準備金率的倒數稱為狹義的貨幣乘數
計算公式
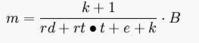 公式
公式m為貨幣存量,B為基礎貨幣,rd為活期存款的法定準備金率,rt為定期存款的法定準備金率,t為定期存款比率,e為超額準備金比率,k為通貨比率。nM1為狹義貨幣; M2為廣義貨幣;B為基礎貨幣;C為現金;D為活期存
款;T為定期存款;E為超額準備金;R為準備金總額。 nm1為狹義貨幣乘數; m2為廣義貨幣乘數;k為通貨比率(現金漏損率);t為定期存款比率;e為超額準備金率;rd為活期存款的法定準備金比率; rt為定期存款的法定準備金比率。nM1=D+C M2 =D+C+T B=R+C c=C/D t=T/D e=E/D —— C=c*D T=t*D E=e*d nM1=D+C=D+ c*D= D(1+c) nM2=D+C+T=D+ c*D+ t*D = D(1+c + t) nB= R+C =[r(D+T )+E]+C= rd*D + rt*T+E+C= rd*D + rt*t*D+e*D+c*D=D(rd + rt*t+e+c) nm1= M1 / B= D(1+c) / D(rd + rt*t+e+c) n = (1+c)/ (rd + rt*t+e+c) nm1= M2 / B= D(1+c+t) / D(rd + rt*t+e+c) n = (1+c+t)/ (rd + rt*t+e+c) nM1=B* m1 = B*(1+c)/ (rd + rt*t+e+c) nM2=B* m2 = B*(1+c+t)/ (rd + rt*t+e+c)
