調和函式
數學物理方程滿足拉普拉斯方程
在某區域中滿足拉普拉斯方程的函式。通常對函式本身還附加一些光滑性條件，例如有連續的一階和二階偏導數。當自變數為n個（從而區域是n維的）時，則稱它為n維調和函式。例如，n=2時,調和函式u(x,y)在某平面區域內滿足方程
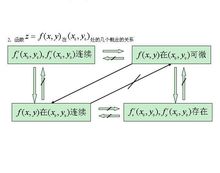二元函式若所考慮的區域包含一個閉圓域，例如x+y≤R，則有下列關於調和函式的平均值公式：
即u(x,y)在圓心的值等於圓周上的積分平均值。
拉普拉斯方程2更一般地，圓內任何一點x=rcosφ，y=rsinφ(0≤r
形如上式右端的積分稱作泊松積分。
設u(x,y)為平面區域G中的調和函式,且在G的閉包上連續,則藉助於平均值公式可以證明,它不能在G 的內部取其最大值與最小值，除非它恆等於一常數。這就是調和函式的最大、最小值原理。
由泊松積分出發可解決下列狄利克雷問題：在區域G的邊界G上給定一連續函式 ƒ(x,y)，要求給出G中的調和函式u(x,y)，使其在嬠G上取ƒ(x,y)的值，即
拉普拉斯方程在G的邊界嬠G滿足一定的條件下,這個問題的解存在且惟一。
對於高維的調和函式，也有與上述類似的最大、最小值原理，平均值公式以及相應的狄利克雷問題解的存在和惟一性定理。
二維調和函式與解析函式論有著密切聯繫。在某區域內的調和函式一定是該區域內某解析函式(可能多值)的實部或虛部；反之，某區域內的解析函式其實部與虛部都是該區域內的調和函式，並稱其虛部為實部的共軛調和函式。用複數z=x+iy的記法,將u(x,y)寫成u(z),若u(z)在│z│
(0≤r
對於任何α,│α│
泊松積分是近代複變函數論中一個重要的研究工具，由此出發，可得出函式論中一系列重要結果。
