正式定義
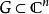 多重調和函式
多重調和函式域名是 使得功能
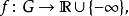 多重調和函式
多重調和函式有 多個分諧波方式是一個(多次調和),它上半一個,所有複雜的線性
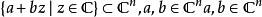 多重調和函式
多重調和函式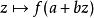 多重調和函式
多重調和函式功能反對 說下一組是次諧波的:
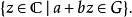 多重調和函式
多重調和函式 多重調和函式
多重調和函式具有完整的一般性,這個概念是一個任意複雜的流形和複雜的分析空間 但可以定義如下。一些上半連續功能
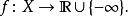 多重調和函式
多重調和函式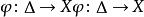 多重調和函式
多重調和函式多次調和條件是一個任意的正則映射 功能反對
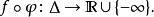 多重調和函式
多重調和函式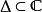 多重調和函式
多重調和函式有劣和諧,不能不說是。這裡 代表一個單位磁碟。
可微分多重劣調和函式
 多重調和函式
多重調和函式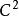 多重調和函式
多重調和函式 多重調和函式
多重調和函式有類(可能有區別) 當屬於 是一個多通道諧波,其必要和充分的條件是組件
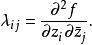 多重調和函式
多重調和函式 多重調和函式
多重調和函式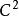 多重調和函式
多重調和函式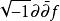 多重調和函式
多重調和函式它是一個半確定的Hermitian矩陣,被稱為Levy矩陣。雖然它是相同的價值, 函式 f是多次諧波的充分必要條件如下: 。
示例
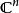 多重調和函式
多重調和函式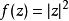 多重調和函式
多重調和函式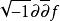 多重調和函式
多重調和函式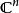 多重調和函式
多重調和函式 多重調和函式
多重調和函式 多重調和函式
多重調和函式與 Kohler流形的關係:n維複數歐幾里德空間 以上 是一個多重調和函式。其實 ,除了時間不變 相當於上面的標準科勒格式。更一般地說, 有一定的科勒格式 另一方面,
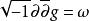 多重調和函式
多重調和函式 多重調和函式
多重調和函式滿意了, 是一個多重分諧波函式,被稱為科勒勢能。
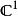 多重調和函式
多重調和函式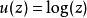 多重調和函式
多重調和函式 多重調和函式
多重調和函式與 狄拉克三角洲的關係:1維複數歐幾里得空間 以上, 是一個多重調和函式。 是一個具有緊湊平台的類函式,從柯西積分公式,
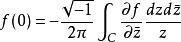 多重調和函式
多重調和函式它可以轉換成以下形式。
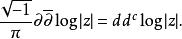 多重調和函式
多重調和函式這是從0開始的狄拉克測量,這不是別的。
歷史
1942年,Okazaki和Pierre Ruong(英文版)定義了多個次諧波函式(多次調和函式 )。
性質
多個次諧波函式(多次調和函式)集在半連續函式向量空間中形成凸錐。即,以下成立。
 多重調和函式
多重調和函式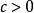 多重調和函式
多重調和函式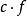 多重調和函式
多重調和函式是一個多重調和函式 如果它是一個正實數, 也是多諧波。
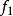 多重調和函式
多重調和函式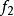 多重調和函式
多重調和函式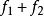 多重調和函式
多重調和函式和 是一個多重分諧波函式,然後求和 也是多諧波。
多重諧度是一個本地屬性。也就是說,該函式是多次諧波的,相當於在每個點附近是多串諧波。
 多重調和函式
多重調和函式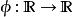 多重調和函式
多重調和函式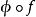 多重調和函式
多重調和函式是多從屬的, 是一個單調遞增的凸函式, 是多從屬的諧波。
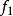 多重調和函式
多重調和函式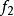 多重調和函式
多重調和函式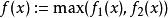 多重調和函式
多重調和函式和 如果它是一個多重諧波函式,一個函式 也是多從屬的。
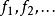 多重調和函式
多重調和函式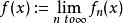 多重調和函式
多重調和函式是一個單調遞減的多重諧波函式系列, 也是一個單調遞減的多次諧波函式。
所有連續的多次諧波函式可以作為單調遞減的一系列平滑多次諧波函式的極限得到。此外,這一行可以被選為統一收斂序列。
 多重調和函式
多重調和函式正態半連續的不等式條件保持為方程。也就是說, 是多排諧波,以下為成立。
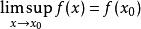 多重調和函式
多重調和函式多重次調和函式是可選的科勒稱重對分諧波方式是。
 多重調和函式
多重調和函式 多重調和函式
多重調和函式 多重調和函式
多重調和函式因此,多個諧波函式滿足最大值原則。也就是說, 有鞏固開放區域 上面是多次諧波,D中的 針對
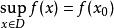 多重調和函式
多重調和函式 多重調和函式
多重調和函式如果它成立, 是一個常數 。