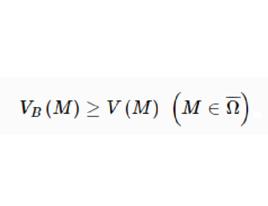定義
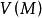 下調和函式
下調和函式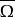 下調和函式
下調和函式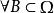 下調和函式
下調和函式定義一:設函式 在 上連續,則對 ,可以定義一個連續函式
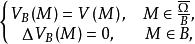 下調和函式
下調和函式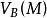 下調和函式
下調和函式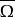 下調和函式
下調和函式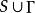 下調和函式
下調和函式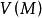 下調和函式
下調和函式即函式 在 上連續,在球 B外部及邊界 上等於 ,在球 B內是 調和函式。
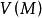 下調和函式
下調和函式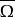 下調和函式
下調和函式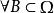 下調和函式
下調和函式定義二:設 在區域 上連續,如果對 ,有
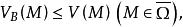 下調和函式
下調和函式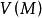 下調和函式
下調和函式 下調和函式
下調和函式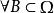 下調和函式
下調和函式則稱 為 上的上調和函式,簡稱 上調和函式;如果對 ,有
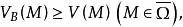 下調和函式
下調和函式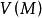 下調和函式
下調和函式 下調和函式
下調和函式則稱 為 上的下調和函式,簡稱 下調和函式。
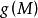 下調和函式
下調和函式 下調和函式
下調和函式 下調和函式
下調和函式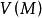 下調和函式
下調和函式定義三:設函式 在 上連續,如果 上的上調和函式 均滿足
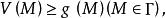 下調和函式
下調和函式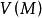 下調和函式
下調和函式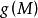 下調和函式
下調和函式 下調和函式
下調和函式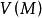 下調和函式
下調和函式則稱 是 的一個 上函式;如果 上的下調和函式 均滿足
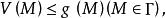 下調和函式
下調和函式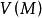 下調和函式
下調和函式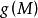 下調和函式
下調和函式則稱是的一個 下函式。
相關性質
性質1
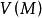 下調和函式
下調和函式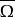 下調和函式
下調和函式 下調和函式
下調和函式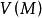 下調和函式
下調和函式設函式 在 上連續,在 內是調和函式,則 既是上調和函式也是下調和函式。
性質2
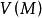 下調和函式
下調和函式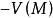 下調和函式
下調和函式設 是上(或下)調和函式,則 是下(或上)調和函式。
性質3
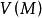 下調和函式
下調和函式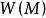 下調和函式
下調和函式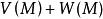 下調和函式
下調和函式設 與 都是上(或下)調和函式,則 也是上(或下)調和函式。
性質4
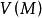 下調和函式
下調和函式 下調和函式
下調和函式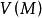 下調和函式
下調和函式 下調和函式
下調和函式設 為 上的上(或下)調和函式,則除 恆等於常數外,它只能在邊界 上取到最小值(或最大值)。
利用上調和函式與下調和函式的定義,容易證明性質1到4。
性質5
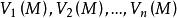 下調和函式
下調和函式設 都是上調和函式,則函式
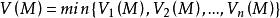 下調和函式
下調和函式也是上調和函式。
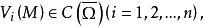 下調和函式
下調和函式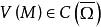 下調和函式
下調和函式證明:由 易知, 。
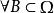 下調和函式
下調和函式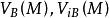 下調和函式
下調和函式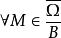 下調和函式
下調和函式另一方面,對 ,由 定義可知,對 ,有
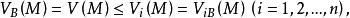 下調和函式
下調和函式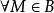 下調和函式
下調和函式並對 ,有
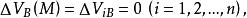 下調和函式
下調和函式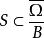 下調和函式
下調和函式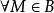 下調和函式
下調和函式故由 ,並根據極值原理可知,對有
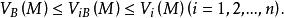 下調和函式
下調和函式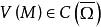 下調和函式
下調和函式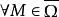 下調和函式
下調和函式綜上可知, ,且對 ,有
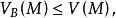 下調和函式
下調和函式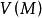 下調和函式
下調和函式 下調和函式
下調和函式即 為 上的上調和函式。
性質6
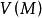 下調和函式
下調和函式 下調和函式
下調和函式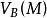 下調和函式
下調和函式設 為 上的上調和函式,則 也是上調和函式。
性質7
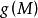 下調和函式
下調和函式 下調和函式
下調和函式 下調和函式
下調和函式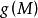 下調和函式
下調和函式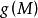 下調和函式
下調和函式設函式 在 的邊界 上連續,則 的任意一個上函式都不小 任意一個下函式。
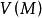 下調和函式
下調和函式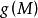 下調和函式
下調和函式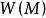 下調和函式
下調和函式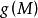 下調和函式
下調和函式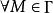 下調和函式
下調和函式證明: 設是的任意一個上函式,是的任意一個下函式,則對,有
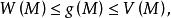 下調和函式
下調和函式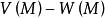 下調和函式
下調和函式 下調和函式
下調和函式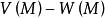 下調和函式
下調和函式 下調和函式
下調和函式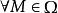 下調和函式
下調和函式並由性質2及性質3可知,是上的上調和函式,故由性質4可知,在上取最小值,即對,有
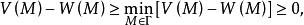 下調和函式
下調和函式 下調和函式
下調和函式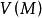 下調和函式
下調和函式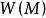 下調和函式
下調和函式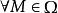 下調和函式
下調和函式從而在內,不小於。即對有
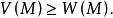 下調和函式
下調和函式性質8
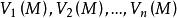 下調和函式
下調和函式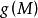 下調和函式
下調和函式設 都是 的上函式,則函式
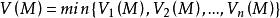 下調和函式
下調和函式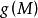 下調和函式
下調和函式也是的上函式。
性質9
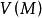 下調和函式
下調和函式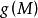 下調和函式
下調和函式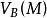 下調和函式
下調和函式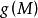 下調和函式
下調和函式設 是 的上函式,則函式 也是 的上函式。