定義
蝴蝶定理最先是作為一個徵求證明的問題,刊載於1815年的一份通俗雜誌《男士日記》上。由於其幾何圖形形象奇特、貌似蝴蝶,便以此命名。
定理內容
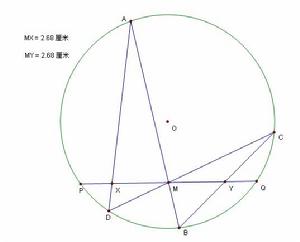
過圓O中的弦PQ的中點M,任作兩弦AB,CD,弦AD與BC分別交PQ於X,Y,則M為XY之中點。
出現過許多優美奇特的解法,其中最早的,應首推霍納在1815年所給出的證法。至於初等數學的證法,在國外資料中,一般都認為是由一位中學教師斯特溫首先提出的,它給予出的是面積證法,其中套用了面積公式:S=1/2 BCSINA。1985年,在河南省《數學教師》創刊號上,杜錫錄同志以《平面幾何中的名題及其妙解》為題,載文向國內介紹蝴蝶定理,從此蝴蝶定理在神州大地到處傳開。
這裡介紹一種較為簡便的初等數學證法。
證明:過圓心O作AD與BC中垂線,垂足為S、T,連線OX,OY,OM。SM。MT。
∵△AMD∽△CMB,且SD=1/2AD,BT=1/2BC,
∴DS/BT=DM/BM又∵∠D=∠B
∴△MSD∽△MTB,∠MSD=∠MTB
∴∠MSX=∠MTY;又∵O,S,X,M與O,T。Y。M均是四點共圓,
∴∠XOM=∠YOM
∵OM⊥PQ∴XM=YM