預備知識
序關係的定義
設R是集合A上的二元關係。如果R是自反、反對稱、傳遞的,那么稱R為A上的序關係(ordered relation)。如果集合A上有序關係R,則稱A為有序集(ordered set),用序偶<A,R>表示。
序關係的關係圖
可對序關係的關係圖進行簡化,操作如下:
(1)由於序關係是自反的,各結點處均有環,約定全部省去;
(2)由於序關係是反對稱且傳遞的,關係圖中任何兩個不同結點之間不可能有相互反方向的邊或通路,因此可約定邊的向上方向為箭頭方向,即若a≤b,則將結點a畫在結點b之下,省略全部箭頭;
(3)由於序關係傳遞,我們還可將由傳遞關係可推定的邊也省去,即若a≤b,b≤c,則肯定應有a≤C,但省略a到c的有向邊;
經過這種簡化的表示序關係的有向圖稱為哈塞(Hasse)圖。哈塞圖既表示一個序關係,又表示一個有序集。
有序集的相關定義
設R是集合A上的二元關係。如果R是A上的序關係,則稱A為有序集(ordered set),用序偶<A,R>表示。 有序集是在其元素之間定義了一個序的集合,例如,一切實數構成的集合、一切整數構成的集合,一切自然數構成的集合等關於通常的大小關係是有序集。 還可表述為,有序集是由一個集合和這個集合中的一種序關係所組成的偶。
 有序集
有序集設<A,≤,>為有序集,B A,則有如下相關定義:
B的最小元、最大元
(1)如果b∈B,且對每一個x∈B,b≤x,則稱b為B的最小元。
(2)如果b∈B,且對每一個x∈B,x≤b,則稱b為B的最大元。
B的極小元、極大元
(1)如果b∈B,並且沒有x∈B,x≠b,使得x≤b,則稱b為B的極小元。
(2)如果b∈B,並且沒有x∈B,x≠b,使得b≤x,則稱b為B的極大元。
B的上界、下界
(1)如果a∈A,且對每一個x∈B,x≤a,則稱a為B的上界。
(2)如果a∈A,且對每一個x∈B,a≤x,則稱a為B的下界。
B的上確界、下確界
(1)如果a是B的所有上界集合的最小元,則稱a為B的最小上界或上確界。
(2)如果a是B的所有下界集合的最大元,則稱a為B的最大下界或下確界。
A上的鏈、反鏈
(1)如果B中的任何兩個元素都是可以比較的,則稱B為A上的鏈;
(2)如果B中的任何兩個不同元素都是不可比較的,則稱B為A上的反鏈。
記|B|為鏈或反鏈的長度。
相似的有序集
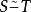 有序集
有序集如果在兩個有序集S和T之間有一個保序的一一對應,則稱兩個有序集S和T是相似的,記作。
相關定理
最元與極元
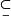 有序集
有序集設<A,≤,>為有序集,B A
(1)若b為B的最大(最小)元,則b為B的極大(極小)元;
(2)若B有最大(最小)元,則B的最大(最小)元唯一;
(3)若B為有限集,則B的極大元、極小元恆存在。
最元與確界
 有序集
有序集設<A,≤,>為有序集,B A
(1)若b為B的最大(最小)元,則b必為B的上(下)確界;
(2)若b為B的上(下)界,且b∈B,則b必為B的最大(最小)元;
(3)如果B有下確界(上確界),則下確界(上確界)唯一。
鏈與反鏈
(1)設<A,≤,>為一個有限的有序集,且A中最長的鏈的長度為n,那么A有一划分,使劃分有n個單元,且每一單元為反鏈。
(2)設<A,≤,>為一個有序集,|A|=mn+1,那么A中或者有m+1(n+1)個元素組成的反鏈,或者有n+1(m+1)個元素的鏈。
光纖通道中的有序集
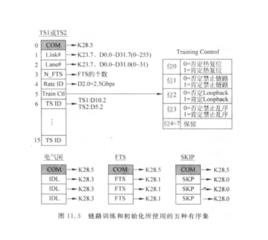
光纖通道中唯一的信息是傳輸中的比特流,我們必須採用一種方法來區分數據比特和各類控制比特,在光纖通道中用有序集來完成這一功能。
結構
光纖通道中的有序集由4個編碼後的位元組共40位組成,開始位元組為控制碼K28.5,其後緊跟3個數據位元組用來定義該有序集的功能。
分類
(1)幀定界符:用來標識數據幀的幀頭和幀尾,例如K28.5 D21.5 D22.2 D22.2有序集可用來標識幀頭,稱之為Start-of-Frame(SOF);K28.5 D21.4 D21.6 D21.6有序集可用來標識幀尾,稱之為End-of-Frame(EOF)。光纖通道定義了11種類型的SOF有序集和8種類型的EOF有序集。
(2)原語信號:用來表示傳輸過程中的動作或事件。主要的原語信號有IDLE原語信號和R_RDY原語信號。IDLE表示為K28.5 D21.4 D21.5 D21.5,用於在沒有數據傳送期間保持鏈路的激活。R_RDY表示為K28.5 D21.4 D10.2 D10.2,用於表示準備在鏈路層傳送幀。
(3)原語序列:用於指示或初始化傳輸中的狀態變化。原語序列包括LIP、OLS、LR、LRR等。