證明過程
證明:因為函式 f(x) 在閉區間[a,b] 上連續,所以存在最大值與最小值,分別用 M 和 m 表示,分兩種情況討論:
1. 若 M=m,則函式 f(x) 在閉區間 [a,b] 上必為常函式,結論顯然成立。
2. 若 M>m,則因為 f(a)=f(b) 使得最大值 M 與最小值 m 至少有一個在 (a,b) 內某點ξ處取得,從而ξ是f(x)的極值點,又條件 f(x) 在開區間 (a,b) 內可導得,f(x) 在 ξ 處取得極值,由費馬引理推知:f'(ξ)=0。
另證:若 M>m ,不妨設f(ξ)=M,ξ∈(a,b),由可導條件知,f'(ξ+)<=0,f'(ξ-)>=0,又由極限存在定理知左右極限均為 0,得證。
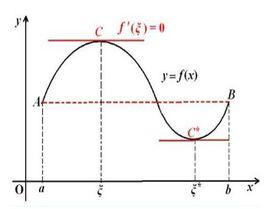
幾何意義
若連續曲線y=f(x) 在區間 [a,b] 上所對應的弧段 AB,除端點外處處具有不垂直於 x 軸的切線,且在弧的兩個端點 A,B 處的縱坐標相等,則在弧 AB 上至少有一點 C,使曲線在C點處的切線平行於 x 軸。
幾種特殊情況
(1)有界開區間上的有界函式
 羅爾中值定理
羅爾中值定理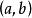 羅爾中值定理
羅爾中值定理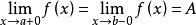 羅爾中值定理
羅爾中值定理 羅爾中值定理
羅爾中值定理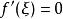 羅爾中值定理
羅爾中值定理若函式 在區間 上連續且可導,並有 ,則至少存在一個 ,使得 。
(2)有界區間上的無界函式
 羅爾中值定理
羅爾中值定理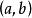 羅爾中值定理
羅爾中值定理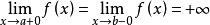 羅爾中值定理
羅爾中值定理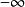 羅爾中值定理
羅爾中值定理 羅爾中值定理
羅爾中值定理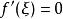 羅爾中值定理
羅爾中值定理若函式 在區間 上連續且可導,並有 (或 ),則至少存在一個 ,使得 。
(3)無界區間上的有界函式
 羅爾中值定理
羅爾中值定理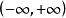 羅爾中值定理
羅爾中值定理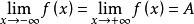 羅爾中值定理
羅爾中值定理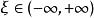 羅爾中值定理
羅爾中值定理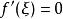 羅爾中值定理
羅爾中值定理若函式 在區間 上連續且可導,並有 ,則至少存在一個 ,使得 。
(4)無界區間上的無界函式
 羅爾中值定理
羅爾中值定理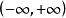 羅爾中值定理
羅爾中值定理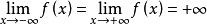 羅爾中值定理
羅爾中值定理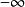 羅爾中值定理
羅爾中值定理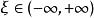 羅爾中值定理
羅爾中值定理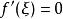 羅爾中值定理
羅爾中值定理若函式 在區間 上連續且可導,並有 (或 ),則至少存在一個 ,使得 。
(5)半無界區間上的有界函式
 羅爾中值定理
羅爾中值定理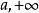 羅爾中值定理
羅爾中值定理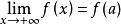 羅爾中值定理
羅爾中值定理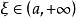 羅爾中值定理
羅爾中值定理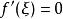 羅爾中值定理
羅爾中值定理若函式 在區間[ )上連續且可導,並有 ,則至少存在一個 ,使得 。
(6)半無界區間上的無界函式
 羅爾中值定理
羅爾中值定理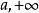 羅爾中值定理
羅爾中值定理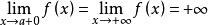 羅爾中值定理
羅爾中值定理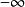 羅爾中值定理
羅爾中值定理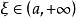 羅爾中值定理
羅爾中值定理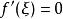 羅爾中值定理
羅爾中值定理若函式 在區間[ )上連續且可導,並有 (或 ),則至少存在一個 ,使得 。
證明
這裡僅選擇特殊情況(2)、(3)加以證明,其餘證明的思路大致類似。
 羅爾中值定理
羅爾中值定理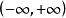 羅爾中值定理
羅爾中值定理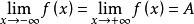 羅爾中值定理
羅爾中值定理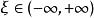 羅爾中值定理
羅爾中值定理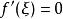 羅爾中值定理
羅爾中值定理定理 若函式 在區間 上連續且可導,並有 。則至少存在一個 ,使得 。
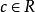 羅爾中值定理
羅爾中值定理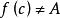 羅爾中值定理
羅爾中值定理 羅爾中值定理
羅爾中值定理 羅爾中值定理
羅爾中值定理 羅爾中值定理
羅爾中值定理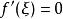 羅爾中值定理
羅爾中值定理證明:至少可取到一點 ,使 ,否則 恆等於 ,對於任意的實數 ,都有 。
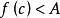 羅爾中值定理
羅爾中值定理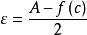 羅爾中值定理
羅爾中值定理 羅爾中值定理
羅爾中值定理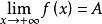 羅爾中值定理
羅爾中值定理不妨設 ,取 ,顯然 。根據極限定義,由 可得
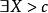 羅爾中值定理
羅爾中值定理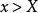 羅爾中值定理
羅爾中值定理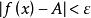 羅爾中值定理
羅爾中值定理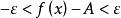 羅爾中值定理
羅爾中值定理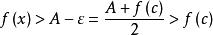 羅爾中值定理
羅爾中值定理,當 時,有 , , ,
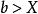 羅爾中值定理
羅爾中值定理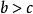 羅爾中值定理
羅爾中值定理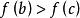 羅爾中值定理
羅爾中值定理任取 ,則有 , 。
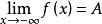 羅爾中值定理
羅爾中值定理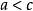 羅爾中值定理
羅爾中值定理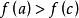 羅爾中值定理
羅爾中值定理利用 ,類似地可知存在 ,使 。
 羅爾中值定理
羅爾中值定理 羅爾中值定理
羅爾中值定理 羅爾中值定理
羅爾中值定理 羅爾中值定理
羅爾中值定理 羅爾中值定理
羅爾中值定理 羅爾中值定理
羅爾中值定理 羅爾中值定理
羅爾中值定理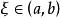 羅爾中值定理
羅爾中值定理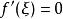 羅爾中值定理
羅爾中值定理於是, 在閉區間 上連續,則在閉區間 上必有 的最小值點 ,由於閉區間 的兩個端點都不可能是 的最小值點,由此可知 ,根據費馬定理可知 。
 羅爾中值定理
羅爾中值定理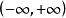 羅爾中值定理
羅爾中值定理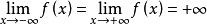 羅爾中值定理
羅爾中值定理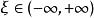 羅爾中值定理
羅爾中值定理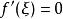 羅爾中值定理
羅爾中值定理定理 若函式 在區間 上連續且可導,並有 。則至少存在一個 ,使得 。
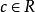 羅爾中值定理
羅爾中值定理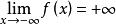 羅爾中值定理
羅爾中值定理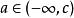 羅爾中值定理
羅爾中值定理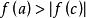 羅爾中值定理
羅爾中值定理證明: 任取 ,因為 ,所以至少存在一點 ,使 。
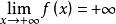 羅爾中值定理
羅爾中值定理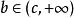 羅爾中值定理
羅爾中值定理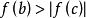 羅爾中值定理
羅爾中值定理類似地由 可知存在一點 ,使 。
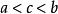 羅爾中值定理
羅爾中值定理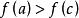 羅爾中值定理
羅爾中值定理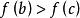 羅爾中值定理
羅爾中值定理這就有了 且 ,
 羅爾中值定理
羅爾中值定理 羅爾中值定理
羅爾中值定理 羅爾中值定理
羅爾中值定理 羅爾中值定理
羅爾中值定理 羅爾中值定理
羅爾中值定理 羅爾中值定理
羅爾中值定理 羅爾中值定理
羅爾中值定理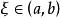 羅爾中值定理
羅爾中值定理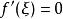 羅爾中值定理
羅爾中值定理於是, 在閉區間 上連續,則在閉區間 上必有 的最小值點 ,由於閉區間 的兩個端點都不可能是 的最小值點,由此可知 ,根據費馬定理可知 。
範例解析
用羅爾中值定理證明:方程
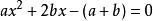 羅爾中值定理
羅爾中值定理3在 (0,1) 內有實根。
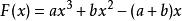 羅爾中值定理
羅爾中值定理證明: 設
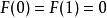 羅爾中值定理
羅爾中值定理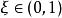 羅爾中值定理
羅爾中值定理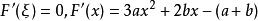 羅爾中值定理
羅爾中值定理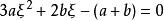 羅爾中值定理
羅爾中值定理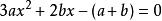 羅爾中值定理
羅爾中值定理則 F(x) 在 [0,1] 上連續,在 (0,1) 內可導,,所以由羅爾中值定理,至少存在一點,使得,所以,所以ξ是方程在 (0,1) 內的一個實根。
結論得證。