定理內容
如果函式f(x)滿足如下條件：
（1）f(x)在閉區間[a ,b]上連續；
（2）f(x)在開區間(a,b) 內可導；
（3）f(x)在區間端點的函式值相等，即f(a)=f(b) ，
那么在(a,b) 內至少有一點ξ (a<ξ<b)，使得函式f(x) 在該點的導數等於零，即f'(ξ)=0。
幾何意義
在每一點都可導的一段連續曲線上，如果曲線的兩端高度相等，則至少存在一條水平切線。（圖形如下所示）
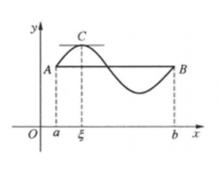幾何意義圖證明過程
因為函式 f(x) 在閉區間[a,b] 上連續，所以存在最大值與最小值，分別用 M 和 m 表示，分兩種情況討論：
（1）若 M=m，則函式 f(x) 在閉區間 [a,b] 上必為常函式，結論顯然成立。
（2）若 M>m，則因為 f(a)=f(b) ，使得最大值 M 與最小值 m 至少有一個在 (a,b) 內某點ξ處取得，從而ξ是f(x)的極值點，又條件 f(x) 在開區間 (a,b) 內可導得，f(x) 在 ξ 處取得極值，由費馬引理推知：f'(ξ)=0。
注意：rolle定理中的三個條件缺少任何一個，結論將不一定成立。
簡單套用
典例1
設f(x)為R上可導函式，證明：若函式f'(x)=0沒有實根，則方程f(x)=0至多只有一個實根。
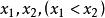rolle定理
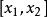rolle定理
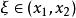rolle定理證明：（反證法）倘若f(x)=0有兩個實根，則函式f在上滿足羅爾定理三個條件，從而存在，使得f'(ξ)=0，這與f'(x)≠0矛盾，故假設不成立，原命題成立。
典例2
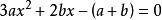rolle定理用羅爾中值定理證明：方程在(0,1)內有實根。
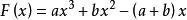rolle定理證明：設
則 F(x) 在 [0,1] 上連續，在 (0,1) 內可導，且F(0)=F(1)。
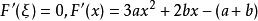rolle定理故由羅爾中值定理，至少存在一點ξ使得F'(ξ)=0;
rolle定理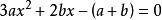 rolle定理故有，即ξ是方程在(0,1)內的實根。命題得證。
