定理
如果函式f(x)滿足下面的條件:(1)在閉區間【a,b】上連續;
(2)在開區間(a,b)內可導;
(3)在區間端點處的函式值相等,即f(a)=f(b),
那么在(a,b)內至少有一點ξ(a<ξ<b),使得 f'(ξ)=0.
證明
根據閉區間連續函式的性質,函式f(x)在區別[a,b]上必有最大值M和最小值m,即存在x1,x2∈[a,b],使得f(x1)=M,f(x2)=m需分成兩種情況來討論:(1)M=m(2)M≠m
(1)當M=m,函式f(x)在區間[a,b]為常數M,於是其導數在區間(a,b)內為0,因此任一f'(ξ)=0;
(2)當M≠m,有條件f(a)=f(b)可知,函式f(x)的最大值或最小值至少有一個在區間(a,b)記憶體在,不妨假設存在最大值。即x1∈(a,b),使得f(x1)=M,根據條件f'(x1)一定存在,並通過證明可知f'(x1)=0。
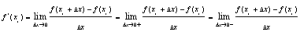 |
| f'(x1)的三種表示 |
後面的兩個極限不等式表明了f'(x1)只能等於0,因此f'(ξ)=f'(x1)=0。
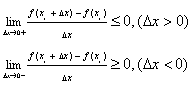 |
| f'(x1)的兩個不等式 |
證明完畢■
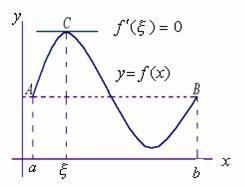
羅爾定理的幾何解釋
羅爾定理的條件表示,曲線弧是一條連續的曲線弧,除端點外處處有不垂直於軸的切線,且兩端點的縱坐標相等。而定理結論表明,
弧上至少有一點,曲線在該點切線是水平的.