微積分
在微積分中, 拉格朗日中值定理是羅爾中值定理的推廣,同時也是柯西中值定理的特殊情形。
1.文字敘述
 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理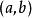 拉格朗日定理
拉格朗日定理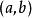 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理如果函式 滿足:1) 在閉區間 上連續;2) 在開區間 內可導;那么在 內至少有一點 ,使等式
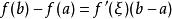 拉格朗日定理
拉格朗日定理成立。
2.邏輯語言的敘述
 拉格朗日定理
拉格朗日定理若函式 滿足:
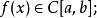 拉格朗日定理
拉格朗日定理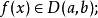 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理則
 拉格朗日定理
拉格朗日定理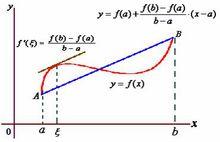 圖1.拉格朗日中值定理的幾何意義
圖1.拉格朗日中值定理的幾何意義3.證明
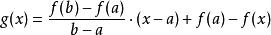 拉格朗日定理
拉格朗日定理令 ,那么
 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理1) 在 上連續,
 拉格朗日定理
拉格朗日定理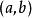 拉格朗日定理
拉格朗日定理2) 在 上可微(導),
 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理3 ,由羅爾定理,存在一點 ,使得 。即 。
數論
1.內容
四平方和定理(Lagrange's four-square theorem) 說明每個正整數均可表示為4個整數的平方和。它是費馬多邊形數定理和華林問題的特例。注意有些整數不可表示為3個整數的平方和,例如7。
2.歷史
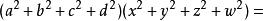 拉格朗日定理
拉格朗日定理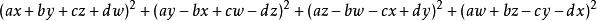 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理1. 1743年,瑞士數學家歐拉發現了一個著名的恆等式:。根據上述歐拉恆等式或四元數的概念可知如果正整數 和 能表示為4個整數的平方和,則其乘積 也能表示為4個整數的平方和。於是為證明原命題只需證明每個素數可以表示成4個整數的平方和即可。
 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理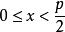 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理2. 1751年,歐拉又得到了另一個一般的結果。即對任意奇素數 ,同餘方程 必有一組整數解 滿足 , (引理一)。
至此,證明四平方和定理所需的全部引理已經全部證明完畢。此後,拉格朗日和歐拉分別在1770年和1773年作出最後的證明。
群論
拉格朗日定理是群論的定理,利用陪集證明了子群的階一定是有限群的階的約數值。
1.定理內容
 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理敘述:設H是有限群 的子群,則 的階整除 的階。
 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理定理的證明是運用 在 中的左陪集。 在 中的每個左陪集都是一個等價類。將 作左陪集分解,由於每個等價類的元素個數都相等,都等於 的元素個數( 是 關於 的左陪集),因此 的階(元素個數)整除 的階,商是 在 中的左陪集個數,叫做 對 的指數,記作 。
陪集的等價關係
 拉格朗日定理
拉格朗日定理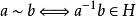 拉格朗日定理
拉格朗日定理定義二元關係 : 。下面證明它是一個等價關係。
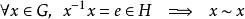 拉格朗日定理
拉格朗日定理1) 自反性: ;
 拉格朗日定理
拉格朗日定理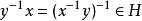 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理2) 對稱性: ,因此 ,因此 ;
 拉格朗日定理
拉格朗日定理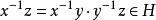 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理3) 傳遞性: ,因此 ,因此 。
 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理可以證明, 。因此左陪集是由等價關係 確定的等價類。
 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理拉格朗日定理說明,如果商群 存在,那么它的階等於 對 的指數 。
 拉格朗日定理
拉格朗日定理2.推論
 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理由拉格朗日定理可立即得到:由有限群 中一個元素 的階數整除群 的階(考慮由 生成的循環群)。
3.逆命題
 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理 拉格朗日定理
拉格朗日定理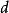 拉格朗日定理
拉格朗日定理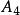 拉格朗日定理
拉格朗日定理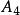 拉格朗日定理
拉格朗日定理拉格朗日定理的逆命題並不成立。給定一個有限群 和一個整除 的階的整數 , 並不一定有階數為 的子群。最簡單的例子是4次交替群 ,它的階是12,但對於12的因數6, 沒有6階的子群。對於這樣的子群的存在性,柯西定理和西洛定理給出了一個部分的回答。

