米氏方程
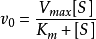米氏方程，這個方程稱為Michaelis-Menten方程，是在假定存在一個穩態反應條件下推導出來的，其中
值稱為米氏常數，
是酶被底物飽和時的反應速度，
為底物濃度。
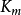米氏方程由此可見
值的物理意義為反應速度
達到
時的底物濃度（即
），單位一般為mol/L，只由酶的性質決定，而與酶的濃度無關。可用
的值鑑別不同的酶。
當底物濃度非常大時，反應速度接近於一個恆定值。在曲線的這個區域，酶幾乎被底物飽和，反應相對於底物S是個零級反應。就是說再增加底物對反應速度沒有什麼影響。
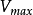米氏方程反應速度逐漸趨近的恆定值稱為最大反應速度
。對於給定酶量的
可以定義為處於飽和底物濃度的起始反應速度n。對於反應曲線的這個假一級反應區的速度方程可寫成一種等價形式：
n（飽和時）=Vmax=k[E][S]0=k[E]total=k cat[ES]
速度常數k等於催化常數k cat，k cat是ES轉化為游離的E和產物的速度常數。飽和時，所有的E都是以ES存在。方程（3.2）中還有另一個簡單的關係式：Vmax=k cat [E]total。從中得出：k cat=Vmax / [E]total。k cat的單位是s－1。催化常數可以衡量一個酶促反應的快慢。
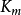米氏方程米氏常數
是酶促反應速度n為最大酶促反應速度值一半時的底物濃度。這可通過用[S]取代米氏方程中的
證明，通過計算可得n=Vmax /2。
方程推導
建立模型
1913年Michaelis L.和Menten M.根據中間複合體學說提出了單底物酶促反應的快速平衡模型或平衡態模型（equilibrium-state model），也稱為米-曼氏模型（Michaelis-Menten model）：
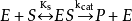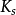米氏方程
米氏方程式中E是酶，S是底物，ES是中間複合體，P是產物，
是ES的解離[平衡]常數，即第一步的逆向反應中的速率常數
和正向速率常數
之比
，
是催化常數，即第二步中的向前速率常數
。
模型假設
在建立模型和推導模型的速率方程時，他們實際上做了以下幾點假設：
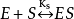米氏方程①為了簡化起見，假設反應中只有一個中間複合體，反應的第一步
是可逆反應，並保持始終；
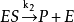米氏方程②反應的第二步
是限速步驟，這裡是限速步驟，這裡
，也就是說ES分解生成P的速率不足以破壞E和ES之間的快速平衡；
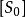米氏方程③為了達到平衡，只用初始底物濃度
的很小一部分，因為一般情況下
（初始酶濃度），因此在反映的初期，底物濃度[S]可以用
代替，或是把[S]看作
；
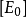米氏方程④酶在反應中不被消耗，只是或以游離形式E存在或以結合形式ES存在，因此游離酶濃度[E]和中間複合體濃度[ES]只和等於初始酶濃度
或總酶濃度
，即
，這就是所謂的酶守恆公式（conservation equation of enzyme）；
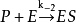米氏方程⑤該模型沒有考慮
這一逆反應，但顯然
是一個不等於零的常數，要忽略這一步，必需使[P]接近於零，因此米-曼氏方程只適用於反應的初速率。
推導過程
根據平衡態模型S轉變成P的總速率應由限速反應（模型中第二步）決定，因此產物生成速率
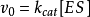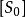米氏方程米氏方程ES複合體的濃度[ES]在實驗上不易測定，需要找出容易測定的其他參數（如某些常數和已知的
等）來代替它。為此利用第一步反應（快速平衡）中ES解離成E和S的解離常數
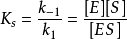米氏方程則
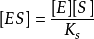米氏方程
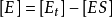米氏方程將酶守恆公式
代入上式得
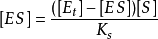米氏方程經整理得
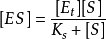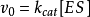米氏方程米氏方程代入
得
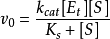米氏方程
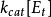米氏方程這裡
具有特殊的意義。當底物濃度[S]高至使所有酶分子都被飽和時，則
，反應初速率
將達到最大值，
用數學式可表示為
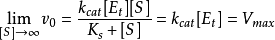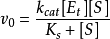米氏方程米氏方程因此
也可寫成
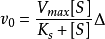米氏方程模型改進
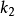米氏方程平衡態模型中前兩點假設不具有普遍性，特別是沒有理由認為所有酶促反應的
都遠小於
。因此1925年Briggs G. E.和Haldane J. B. S.對該模型提出了修正，但仍保留米-曼氏假設的後三點。他們用穩態模型（steady-state model）或稱Briggs-Haldane氏模型：
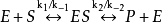米氏方程
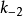米氏方程代替了平衡態模型。對觀測初速率（即產物P尚未生成或很少生成時）來說，式中仍可忽略不計。所謂穩態是指反應進行不成的一段時間內（順便提及，幾毫秒內，這段時間的狀態稱為前穩態），系統中[ES]由零增加到一定值，在一定時間內雖然[S]和[P]在不斷變化，ES複合體也在不斷地生成和分解，但ES的生成速率
與分解速率
接近相等，[ES]基本保持不變。因此在穩態下ES形成的淨速率，
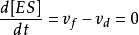米氏方程
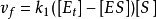米氏方程因為
且
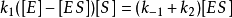米氏方程所以
整理得
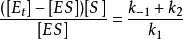米氏方程
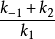米氏方程這裡，速率是常數之比
本身也是一個常數，並被定義為米氏常數（Michaelis constant），
：
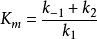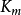米氏方程米氏方程將
代入
，整理得：
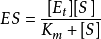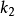米氏方程米氏方程根據穩態模型，S轉變為P的速率決定於穩態濃度[ES]和限速的速率常數
。因此
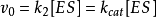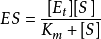米氏方程米氏方程將
代入上式，得
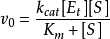米氏方程或
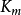米氏方程米氏方程根據兩種模型推導出的速率方程形式上是一樣的，兩者不同的是
比
具有更大的普遍性。穩態下，當
時，則
，因此可以把平衡態看成是穩態的一個特例。為了紀念Michaelis和Menten兩人，人們把上述帶三角符號的的方程都稱為米-曼氏方程（Michaelis-Menten equation）。
參數意義
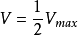米氏方程①當
時，
。因此，Km等於酶促反應速度達最大值一半時的底物濃度。
米氏方程②當
時，
=Ks。因此，Km可以反映酶與底物親和力的大小，即
值越小，則酶與底物的親和力越大；反之，則越小。
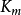米氏方程③
可用於判斷反應級數：當[S]<0.01Km時，ν=（Vmax/Km）[S]，反應為一級反應，即反應速度與底物濃度成正比；當[S]>100Km時，ν=Vmax，反應為零級反應，即反應速度與底物濃度無關；當0.01Km<[S]<100Km時，反應處於零級反應和一級反應之間，為混合級反應。
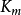米氏方程④
是酶的特徵性常數：在一定條件下，某種酶的Km值是恆定的，因而可以通過測定不同酶（特別是一組同工酶）的Km值，來判斷是否為不同的酶。
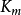米氏方程⑤
可用來判斷酶的最適底物：當酶有幾種不同的底物存在時，Km值最小者，為該酶的最適底物。
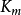米氏方程⑥
可用來確定酶活性測定時所需的底物濃度：當[S]=10Km時，ν=91%Vmax，為最合適的測定酶活性所需的底物濃度。
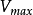米氏方程⑦
可用於酶的轉換數的計算：當酶的總濃度和最大速度已知時，可計算出酶的轉換數，即單位時間內每個酶分子催化底物轉變為產物的分子數。
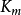米氏方程⑷
和
的測定：主要採用Lineweaver-Burk雙倒數作圖法和Hanes作圖法。
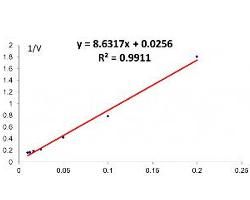
雙倒數圖
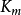米氏方程酶促反應中的
和
值有幾種測量方法。固定反應中的酶濃度，然後分析幾種不同底物濃度下的起始速度，就可獲得
和
值。但直接從起始速度對底物濃度的圖中確定Km或
值是很困難的，因為曲線接近
時是個漸進過程。所以通常都是利用米氏方程的轉換形式求出Km和
值。常用的米氏方程轉換形式是Lineweaver-Burk方程，也稱為雙倒數方程。
使1/ v 對1/[S]作圖，可以獲得一條直線。從直線與x軸的截距可以得到1/Km的絕對值；而1/Vmax是直線與y軸的截距。雙倒數作圖直觀、容易理解，為酶抑制研究提供了易於識別的圖形。
缺點：底物濃度低時，坐標點集中於坐標左下方，使得誤差增大，往往偏離直線，Vm、Km無法精確定出。
解決方法：底物濃度配成1/[S]的濃度級差，而不是[S]的濃度極差，使點距離平均，再以最小二乘法線性回歸分析。
抑制作用
競爭性抑制
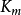米氏方程值增大，
值不變
非競爭性抑制
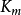米氏方程值不變，
值變小
反競爭性抑制
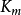米氏方程值變小，
值變小，但
值不變
酶相關名詞
酶 | 酶動力學 | 催化常數 | 酵素梅 | 競爭性抑制 | 非特異性抑制劑 | 酶多重性 | 多酶體系 | 開特 | 全酶 | 米氏常數 | 酶催化機制 | 催化部位 | 非競爭性抑制 | 抑制結構域 | 酶多態性 | 多酶複合物 | 活化能 | 米氏方程 | 鎖鑰學說 | 催化亞基 | 反競爭性抑制 | 協同催化 | 酶解作用 | 活性部位 | 同工酶 | 米氏動力學 | 誘導契合學說 | 不可逆抑制 | 非特異性抑制 | 協作抑制 |酶複合物| 酶活性 | 最適pH | 酶原 | 雙倒數作圖法 | 催化活性 | 可逆抑制 | 競爭性抑制劑 | 反饋抑制 | 酶系 | 酶單位 | 最適溫度
