矩形的判定
1.有三個角是直角的四邊形是矩形;
2.對角線互相平分且相等的四邊形是矩形;
3.有一個角為直角的平行四邊形是矩形;
4.對角線相等的平行四邊形是矩形。
套用舉例
 1
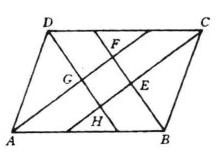
1例1 試證平行四邊形四個內角平分線所圈成的四邊形是矩形 。
已知:如圖,平行四邊形ABCD的四個內角平分線的交點為E、F、G、H,
求證:四邊形EFGH是矩形。
證明:因為四邊形ABCD是平行四邊形.所以∠DAB+∠CBA=180°。
因為AF、BF分別是∠DAB、∠CBA的平分線,所以∠FAB+∠FBA=90°。
在△FAB中,得∠AFB=90°。同理 ∠DHC=90°,∠FGH=90°。
所以四邊形EFGH是矩形。
例2 如圖,已知:AB⊥BC,DC⊥BC,MA=MD,∠AMB=75°,∠DMC=45°,求證:AB=BC。
 2
2證明:作DE⊥AB,垂足為E。
因為∠AMD=180°一75°一45°=60°,MA=MD,
所以△AMD是等邊三角形。
又因為∠EAD=60°+15°=75°=∠BMA,
所以Rt△ABM≌Rt△DEA。所以AB=DE。
因為∠DEB=∠B=∠C=90°,
所以四邊形BCDE為矩形。
所以BC=DE。
所以AB=BC .
相關概念
矩形定義
有一個角是直角的平行四邊形叫矩形 。
性質
性質定理1:矩形的四個角都是直角;
性質定理2:矩形的對角線相等。
判定
判定定理1:有三個角是直角的四邊形是矩形;
判定定理2:對角線相等的平行四邊形是矩形。
周長和面積公式
如下圖,矩形ABCD的周長C=2(a+b);矩形ABCD的面積S=ab。(當a=b時,可以得到正方形的相應公式)