公式
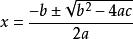八年級下冊數學定理
1、分式定義：如果A、B表示兩個整式，並且B中含有字母，那么式子A/B叫做分式，
分式有意義的條件是分母不為零，分式值為零的條件分子為零且分母不為零
2、分式的基本性質：分式的分子與分母同乘或除以一個不等於0的整式，分式的值不變
3、分式的通分和約分：關鍵先是求分母的最低公倍數和分解因式
4、同角或等角的餘角相等
5、過一點有且只有一條直線和已知直線垂直
6、平行公理 經過直線外一點，有且只有一條直線與這條直線平行
7、如果兩條直線都和第三條直線平行，這兩條直線也互相平行
8、同位角相等，兩直線平行
9、同旁內角互補，兩直線平行
10、兩直線平行，同位角相等
11、定理 ：三角形兩邊的和大於第三邊
16 、推論 ：三角形兩邊的差小於第三邊
17、三角形內角和定理：三角形三個內角的和等於180°
18 、推論1 ：直角三角形的兩個銳角互余
19 、推論2 ：三角形的一個外角等於和它不相鄰的兩個內角的和
20 、推論3 ：三角形的一個外角大於任何一個和它不相鄰的內角
21 、全等三角形的對應邊、對應角相等
22、邊角邊公理(SAS) 有兩邊和它們的夾角對應相等的兩個三角形全等
23 、角邊角公理( ASA)有兩角和它們的夾邊對應相等的兩個三角形全等
24 、推論(AAS) 有兩角和其中一角的對邊對應相等的兩個三角形全等
25 、邊邊邊公理(SSS) 有三邊對應相等的兩個三角形全等
26、斜邊、直角邊公理(HL) 有斜邊和一條直角邊對應相等的兩個直角三角形全等
27 、定理1 ：在角的平分線上的點到這個角的兩邊的距離相等
28 、定理2 ：到一個角的兩邊的距離相同的點，在這個角的平分線上
29 、角的平分線是到角的兩邊距離相等的所有點的集合
30 、等腰三角形的性質定理 等腰三角形的兩個底角相等 (即等邊對等角）
31 、推論1 ：等腰三角形頂角的平分線平分底邊並且垂直於底邊
32 、等腰三角形的頂角平分線、底邊上的中線和底邊上的高互相重合
33 、推論3 ：等邊三角形的各角都相等，並且每一個角都等於60°
34 、等腰三角形的判定定理 ：如果一個三角形有兩個角相等，那么這兩個角所對的邊也相等（等角對等邊）
35、 推論1 ：三個角都相等的三角形是等邊三角形
36 、推論2 ：有個角等於60°的等腰三角形是等邊三角形
37 、在直角三角形中，如果一個銳角等於30°那么它所對的直角邊等於斜邊的一半
38 、直角三角形斜邊上的中線等於斜邊上的一半
39 、定理 ：線段垂直平分線上的點和這條線段兩個端點的距離相等
40 、逆定理 ：和一條線段兩個端點距離相等的點，在這條線段的垂直平分線上
41 、線段的垂直平分線可看作和線段兩端點距離相等的所有點的集合
42 、定理1 ：關於某條直線對稱的兩個圖形是全等形
43 、定理 2 ：如果兩個圖形關於某直線對稱，那么對稱軸是對應點連線的垂直平分線
44、定理3 ：兩個圖形關於某直線對稱，如果它們的對應線段或延長線相交，那么交點在對稱軸上
45、逆定理 ：如果兩個圖形的對應點連線被同一條直線垂直平分，那么這兩個圖形關於這條直線對稱
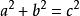八年級下冊數學46、勾股定理 ：直角三角形兩直角邊a、b的平方和、等於斜邊c的平方，即
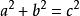八年級下冊數學47、勾股定理的逆定理：如果三角形的三邊長a、b、c有關係 ，那么這個三角形是直角三角形
48、定理 ：四邊形的內角和等於360°
49、四邊形的外角和等於360°
50、多邊形內角和定理：n邊形的內角的和等於（n-2）×180°
51、推論 ：任意多邊的外角和等於360°
52、平行四邊形性質定理1 ：平行四邊形的對角相等
53、平行四邊形性質定理2 ：平行四邊形的對邊相等
54、推論 ：夾在兩條平行線間的平行線段相等
55、平行四邊形性質定理3 ：平行四邊形的對角線互相平分
56、平行四邊形判定定理1 ：兩組對角分別相等的四邊形是平行四邊形
57、平行四邊形判定定理2 ：兩組對邊分別相等的四邊形是平行四邊形
58、平行四邊形判定定理3 ：對角線互相平分的四邊形是平行四邊形
59、平行四邊形判定定理4 ：一組對邊平行相等的四邊形是平行四邊形
60、矩形性質定理1 ：矩形的四個角都是直角
61、矩形性質定理2 ：矩形的對角線相等
62、矩形判定定理1 ：有三個角是直角的四邊形是矩形
63、矩形判定定理2 ：對角線相等的平行四邊形是矩形
64、菱形性質定理1： 菱形的四條邊都相等
65、菱形性質定理2 ：菱形的對角線互相垂直，並且每一條對角線平分一組對角
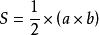八年級下冊數學66、菱形面積=對角線乘積的一半，即
67、菱形判定定理1： 四邊都相等的四邊形是菱形
68、菱形判定定理2 ：對角線互相垂直的平行四邊形是菱形
69、正方形性質定理1 ：正方形的四個角都是直角，四條邊都相等
70、正方形性質定理2：正方形的兩條對角線相等，並且互相垂直平分，每條對角線平分一組對角
71、定理1 ：關於中心對稱的兩個圖形是全等的
72、定理2 ：關於中心對稱的兩個圖形，對稱點連線都經過對稱中心，並且被對稱中心平分
73、逆定理 ：如果兩個圖形的對應點連線都經過某一點，並且被這一
點平分，那么這兩個圖形關於這一點對稱
74、等腰梯形性質定理：等腰梯形在同一底上的兩個角相等
75、等腰梯形的兩條對角線相等
76、等腰梯形判定定理：在同一底上的兩個角相等的梯形是等腰梯形
77、對角線相等的梯形是等腰梯形
78、平行線等分線段定理：如果一組平行線在一條直線上截得的線段
相等，那么在其他直線上截得的線段也相等
79、 推論1 ：經過梯形一腰的中點與底平行的直線，必平分另一腰
80 、推論2 ：經過三角形一邊的中點與另一邊平行的直線，必平分第
三邊
81、三角形中位線定理：三角形的中位線平行於第三邊，並且等於它
的一半
82、梯形中位線定理：梯形的中位線平行於兩底，並且等於兩底和的
一半 L=（a+b）÷2 S=L×h
83、 (1)比例的基本性質 如果a:b=c:d,那么ad=bc
如果ad=bc,那么a:b=c:d
84 、(2)合比性質 如果a/b=c/d,那么(a±b)/b=(c±d)/d
85 、(3)等比性質 如果a/b=c/d=…=m/n(b+d+…+n≠0),那么
(a+c+…+m)/(b+d+…+n)=a/b
基本公式
乘法與因式分解 a2-b2=(a+b)(a-b)、 a3+b3=(a+b)(a2-ab+b2) 丶a3-b3=(a-b)(a2+ab+b2)
三角不等式 |a+b|≤|a|+|b|、 |a-b|≤|a|+|b|、 |a|≤b<=>-b≤a≤b、
|a-b|≥|a|-|b| -|a|≤a≤|a|
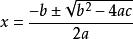八年級下冊數學一元二次方的解
根與係數的關係 註：韋達定理
判別式
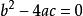八年級下冊數學註：方程有兩個相等的實根
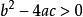八年級下冊數學註：方程有兩個不等的實根
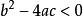八年級下冊數學註：方程沒有實根，有共軛複數根
某些數列前n項和
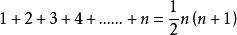八年級下冊數學
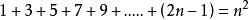八年級下冊數學，
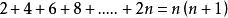八年級下冊數學
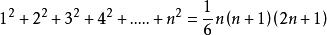八年級下冊數學，
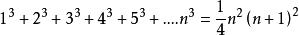八年級下冊數學，
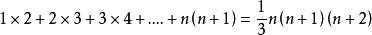八年級下冊數學其他
定理
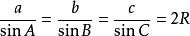八年級下冊數學正弦定理 註： 其中 R 表示三角形的外接圓半徑
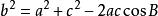八年級下冊數學餘弦定理 註：角B是邊a和邊c的夾角
方程
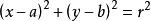八年級下冊數學圓的標準方程 註：（a,b）是圓心坐標
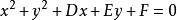八年級下冊數學
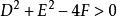八年級下冊數學圓的一般方程 註：
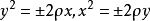八年級下冊數學拋物線標準方程
面積計算
直稜柱側面積 S=c*h 斜稜柱側面積 S=c'*h
正稜錐側面積 S=1/2c*h' 正稜台側面積 S=1/2(c+c')h'
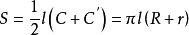八年級下冊數學
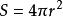八年級下冊數學圓台側面積 球的表面積
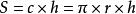八年級下冊數學
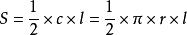八年級下冊數學圓柱側面積 圓錐側面積
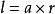八年級下冊數學
八年級下冊數學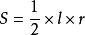
八年級下冊數學弧長公式 是圓心角的弧度數r >0 扇形面積公式
分章解析
1.分式定義：如果A、B表示兩個整式，並且B中含有字母，那么式子A/B叫做分式。
分式有意義的條件是分母不為零，分式值為零的條件分子為零且分母不為零
2.分式的基本性質：分式的分子與分母同乘或除以一個不等於0的整式，分式的值不變。
3.分式的通分和約分：關鍵先是求分母的最低公倍數和分解因式
4.分式的運算：分式乘法法則：兩分式分子分母分別相乘，作為結果的分子分母，能約分的要約成最簡結果。
分式除法法則：分式除以分式，把除式的分子、分母顛倒位置後，與被除式相乘。
分式乘方法則： 分式乘方要把分子、分母分別乘方。
分式的加減法則：同分母的分式相加減，分母不變，把分子相加減。異分母的分式相加減，先通分，變為同分母分式，然後再加減
混合運算:運算順序和以前一樣。能用運算率簡算的可用運算率簡算。
5. 任何一個不等於零的數的零次冪等於1， 即 ；當n為正整數時， （
正整數指數冪運算性質（請同學們自己複習）也可以推廣到整數指數冪．
6. 分式方程：含分式，並且分母中含未知數的方程——分式方程。
解分式方程的過程，實質上是將方程兩邊同乘以一個整式（最簡公分母），把分式方程轉化為整式方程。
解分式方程時，方程兩邊同乘以最簡公分母時，最簡公分母有可能為0，這樣就產生了增根，因此分式方程一定要驗根。
解分式方程的步驟 ：
(1)能化簡的先化簡(2)方程兩邊同乘以最簡公分母，化為整式方程；(3)解整式方程；(4)驗根．
增根應滿足兩個條件：一是其值應使最簡公分母為0，二是其值應是去分母后所的整式方程的根。
分式方程檢驗方法：將整式方程的解帶入最簡公分母，如果最簡公分母的值不為0，則整式方程的解是原分式方程的解；否則，這個解不是原分式方程的解。
列方程套用題的步驟是什麼？ (1)審；(2)設；(3)列；(4)解；(5)答．
套用題有幾種類型；基本公式是什麼？基本上有五種： (1)行程問題：基本公式：路程=速度×時間而行程問題中又分相遇問題、追及問題． (2)數字問題 在數字問題中要掌握十進制數的表示法． (3)工程問題 基本公式：工作量=工時×工效． (4)順水逆水問題 v順水=v靜水+v水． v逆水=v靜水-v水．
7.科學記數法：把一個數表示成 的形式（其中 ，n是整數）的記數方法叫做科學記數法．
用科學記數法表示絕對值大於10的n位整數時，其中10的指數是
用科學記數法表示絕對值小於1的正小數時,其中10的指數是第一個非0數字前面0的個數(包括小數點前面的一個0)
反比例函式
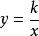八年級下冊數學1.定義：形如 （k為常數，k≠0）的函式稱為反比例函式。
2.圖像：反比例函式的圖像屬於雙曲線。
3.性質:當k>0時雙曲線的兩支分別位於第一、第三象限，在每個象限內y值隨x值的增大而減小；
當k<0時雙曲線的兩支分別位於第二、第四象限，在每個象限內y值隨x值的增大而增大。
4.|k|的幾何意義：表示反比例函式圖像上的點向兩坐標軸所作的垂線段與兩坐標軸圍成的矩形的面積。
勾股定理
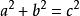八年級下冊數學1.勾股定理：如果直角三角形的兩直角邊長分別為a，b，斜邊長為c，那么 。
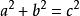八年級下冊數學2.勾股定理逆定理：如果三角形三邊長a,b,c滿足 。，那么這個三角形是直角三角形。
3.經過證明被確認正確的命題叫做定理。
我們把題設、結論正好相反的兩個命題叫做互逆命題。如果把其中一個叫做原命題，那么另一個叫做它的逆命題。（例：勾股定理與勾股定理逆定理）
四邊形
平行四邊形定義： 有兩組對邊分別平行的四邊形叫做平行四邊形。
平行四邊形的性質：平行四邊形的對邊相等；平行四邊形的對角相等。平行四邊形的對角線互相平分。
平行四邊形的判定1.兩組對邊分別相等的四邊形是平行四邊形2.對角線互相平分的四邊形是平行四邊形；
3.兩組對角分別相等的四邊形是平行四邊形； 4.一組對邊平行且相等的四邊形是平行四邊形。
三角形的中位線平行於三角形的第三邊，且等於第三邊的一半。
直角三角形斜邊上的中線等於斜邊的一半。
矩形的定義：有一個角是直角的平行四邊形。
矩形的性質： 矩形的四個角都是直角；矩形的對角線平分且相等。
矩形判定定理： 1.有一個角是直角的平行四邊形叫做矩形。 2.對角線相等的平行四邊形是矩形。
3.有三個角是直角的四邊形是矩形。
菱形的定義 ：鄰邊相等的平行四邊形。
菱形的性質：菱形的四條邊都相等；菱形的兩條對角線互相垂直平分，並且每一條對角線平分一組對角。
菱形的判定定理： 1.一組鄰邊相等的平行四邊形是菱形。 2.對角線互相垂直的平行四邊形是菱形。
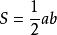八年級下冊數學3.四條邊相等的四邊形是菱形。 （a、b為兩條對角線）
正方形定義：一個角是直角的菱形或鄰邊相等的矩形。有一個角是直角三邊相等的平行四邊形是正方形。
正方形的性質：四條邊都相等，四個角都是直角。 正方形既是矩形，又是菱形。
正方形判定定理： 1.鄰邊相等的矩形是正方形。 2.有一個角是直角的菱形是正方形。
梯形的定義： 一組對邊平行，另一組對邊不平行的四邊形叫做梯形。
直角梯形的定義：有一個角是直角的梯形
等腰梯形的定義：兩腰相等的梯形。
等腰梯形的性質：等腰梯形同一底邊上的兩個角相等；等腰梯形的兩條對角線相等。
等腰梯形判定定理：同一底上兩個角相等的梯形是等腰梯形。
解梯形問題常用的輔助線：如圖
線段的重心就是線段的中點。平行四邊形的重心是它的兩條對角線的交點。 三角形的三條中線交於疑點，這一點就是三角形的重心。 寬和長的比是 （約為0.618）的矩形叫做黃金矩形。
數據的分析
1.加權平均數：加權平均數的計算公式。 權的理解:反映了某個數據在整個數據中的重要程度。
學會權沒有直接給出數量，而是以比的或百分比的形式出現及頻數分布表求加權平均數的方法。
2.將一組數據按照由小到大（或由大到小）的順序排列，如果數據的個數是奇數，則處於中間位置的數就是這組數據的中位數(median)；如果數據的個數是偶數，則中間兩個數據的平均數就是這組數據的中位數。
3.一組數據中出現次數最多的數據就是這組數據的眾數（mode）。
4.一組數據中的最大數據與最小數據的差叫做這組數據的極差(range)。
5. 方差越大，數據的波動越大；方差越小，數據的波動越小，就越穩定。
數據的收集與整理的步驟：1.收集數據 2.整理數據 3.描述數據 4.分析數據 5.撰寫調查報告 6.交流
6. 平均數受極端值的影響眾數不受極端值的影響，這是一個優勢，中位數的計算很少不受極端值的影響。
