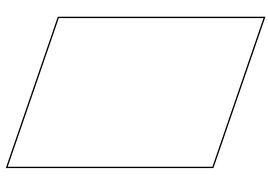
定義：
有兩組對邊分別平行的四邊形叫做 平行四邊形，包括長方形、菱形、正方形和一般平行四邊形，其邊與邊、角與角、對角線之間存在著各種各樣的關係，即是 平行四邊形性質定理。
性質
兩組對邊平行且相等；
兩組對角大小相等；
相鄰的兩個角互補；
對角線互相平分；
對於平面上任何一點，都存在一條能將平行四邊形平分為兩個面積相等圖形、並穿過該點的線；
四邊邊長的平方和等於兩條對角線的平方和 。
1.兩組對邊平行且相等；
2.兩組對角大小相等；
3.相鄰的兩個角互補；
4.對角線互相平分；
5.對於平面上任何一點，都存在一條能將平行四邊形平分為兩個面積相等圖形、並穿過該點的線；
6.四邊邊長的平方和等於兩條對角線的平方和 。
分類
矩形、菱形、正方形是特殊的平行四邊形。
判定定理：
（1）定義法：兩組對邊分別平行的四邊形是平行四邊形；
（2）兩組對邊分別相等的四邊形是平行四邊形；
（3）兩組對角分別相等的四邊形是平行四邊形；
（4）對角線互相平分的四邊形是平行四邊形；
（5）一組對邊平行且相等的四邊形是平行四邊形。
面積
公式一：
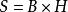平行四邊形性質定理公式二：
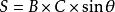平行四邊形性質定理公式三：
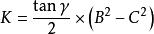平行四邊形性質定理其中，γ是對角線夾角，B,C為兩條鄰邊。
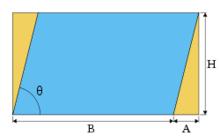圖1.圖中藍色區域為平行四邊形的面積平行四邊形恆等式
平行四邊形性質定理平行四邊形恆等式是描述平行四邊形的幾何特性的一個恆等式。它等價於三角形的中線定理。在一般的賦范內積空間（也就是定義了長度和角度的空間）中，也有類似的結果。這個等式的最簡單的情形是在普通的平面上：一個平行四邊形的兩條對角線長度的平方和，等於它四邊長度的平方和。假設這個平行四邊形是寫作 的話，那么平行四邊形恆等式就可以寫成：
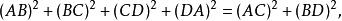平行四邊形性質定理當平行四邊形是矩形的時候，由矩形的幾何特性可以知，這時兩條對角線是一樣長的。所以平行四邊形恆等式變為：
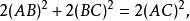平行四邊形性質定理也就是直角三角形的勾股定理：
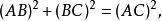平行四邊形性質定理也就是說，平面上的平行四邊形恆等式可以看成是勾股定理的一種推廣 。
