特徵分解

對應的特徵向量。 為矩陣的特徵多項式。 的特徵向量 。

基礎理論

N 維非零向量 v 是 N×N 的矩陣 A 的特徵向量，若且唯若下式成立：
\mathbf{A} \mathbf{v} = \lambda \mathbf{v}
其中 λ 為一標量，稱為 v 對應的特徵值。也稱 v 為特徵值 λ 對應的特徵向量。也即特徵向量被施以線性變換 A 只會使向量伸長或縮短而其方向不被改變。
由上式可得 p\left(\lambda\right) := \det\left(\mathbf{A} - \lambda \mathbf{I}\right)= 0. \!\
稱多項式 p(λ) 為矩陣的特徵多項式。上式亦稱為矩陣的特徵方程。特徵多項式是關於未知數 λ 的 N 次多項式。由代數基本定理，特徵方程有 N 個解。這些解的解集也就是特徵值的集合，有時也稱為“譜”（Spectrum）。
我們可以對多項式 p 進行因式分解，而得到
p\left(\lambda\right)= (\lambda-\lambda_1)^{n_1}(\lambda-\lambda_2)^{n_2}\cdots(\lambda-\lambda_k)^{n_k} = 0 \!\
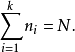
其中\sum\limits_{i=1}^{k}{n_i} =N.
對每一個特徵值 λi ，我們都有下式成立：
\left(\mathbf{A} - \lambda_i \mathbf{I}\right)\mathbf{v} = 0. \!\
對每一個特徵方程，都會有m_i（1\le m_i \le n_i）個線性無關的解。這 mi 個向量與一個特徵值 λi 相對應。這裡，整數 mi 稱為特徵值 λi 的幾何重數，而 ni 稱為代數重數。這裡需要注意的是幾何重數與代數重數可以相等，但也可以不相等。一種最簡單的情況是 mi = ni = 1。特徵向量的極大線性無關向量組中向量的個數可以由所有特徵值的幾何重數之和來確定。

分解方法

矩陣的特徵分解

令 A 是一個 N×N 的方陣，且有 N 個線性無關的特徵向量q_i \,\, (i = 1, \dots, N)。這樣， A 可以被分解為
\mathbf{A}=\mathbf{Q}\mathbf{\Lambda}\mathbf{Q}^{-1}
其中 Q 是N×N方陣，且其第 i列為 A 的特徵向量 。 Λ 是對角矩陣，其對角線上的元素為對應的特徵值，也即\Lambda_{ii}=\lambda_i。這裡需要注意只有可對角化矩陣才可以作特徵分解。比如\begin{bmatrix}1 1 \\0 1 \\\end{bmatrix}不能被對角化，也就不能特徵分解。
一般來說，特徵向量q_i \,\, (i = 1, \dots, N)一般被正交單位化（但這不是必須的）。未被正交單位化的特徵向量組v_i \,\, (i = 1, \dots, N),也可以作為 Q 的列向量。這一事實可以這樣理解： Q 中向量的長度都被Q^{-1}抵消了。
  • 通過特徵分解求矩陣的逆

若矩陣 A 可被特徵分解並特徵值中不含零，則矩陣 A 為非奇異矩陣，且其逆矩陣可以由下式給出：
\mathbf{A}^{-1}=\mathbf{Q}\mathbf{\Lambda}^{-1}\mathbf{Q}^{-1}
因為 Λ 為對角矩陣，其逆矩陣容易計算出：
\left[\Lambda^{-1}\right]_{ii}=\frac{1}{\lambda_i}

對特殊矩陣的特徵分解

  • 對稱矩陣

任意的 N×N 實對稱矩陣都有 N 個線性無關的特徵向量。並且這些特徵向量都可以正交單位化而得到一組正交且模為 1 的向量。故實對稱矩陣 A 可被分解成
\mathbf{A}=\mathbf{Q}\mathbf{\Lambda}\mathbf{Q}^{T}
其中 Q 為 正交矩陣， Λ 為實對角矩陣。
  • 正規矩陣

類似地，一個復正規矩陣具有一組正交特徵向量基，故正規矩陣可以被分解成
\mathbf{A}=\mathbf{U}\mathbf{\Lambda}\mathbf{U}^{H}
其中 U 為一個酉矩陣。進一步地，若 A 是埃爾米特矩陣，那么對角矩陣 Λ 的對角元全是實數。若 A 還是酉矩陣，則 Λ 的所有對角元在複平面的單位圓上取得。

相關詞條

熱門詞條

聯絡我們