定義
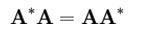 符合該條件的矩陣為正規矩陣
符合該條件的矩陣為正規矩陣即:
符合該條件的矩陣為正規矩陣
符合該條件的矩陣為正規矩陣
其中A*是A的共軛轉置。
矩陣的正規性是檢驗矩陣是否可對角化的一個簡便方法:任意正規矩陣都可在經過一個酉變換後變為對角矩陣,反過來所有可在經過一個酉變換後變為對角矩陣的矩陣都是正規矩陣。
性質
正規矩陣的性質:屬於正規矩陣不同特徵值的特徵向量兩兩正交。
定理1:在複數域上,A為正規矩陣的充分必要條件為A有n個兩兩正交的單位特徵向量
定理2:在複數域上,A為正規矩陣的充分必要條件為A酉相似於對角矩陣
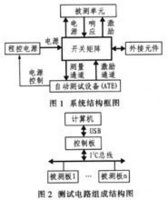
在數學中,正規矩陣是與自己的共軛轉置矩陣對易的復係數方塊矩陣。矩陣的正規性是檢驗矩陣是否可對角化的一個簡便方法。
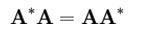 符合該條件的矩陣為正規矩陣
符合該條件的矩陣為正規矩陣正規矩陣的性質:屬於正規矩陣不同特徵值的特徵向量兩兩正交。
定理1:在複數域上,A為正規矩陣的充分必要條件為A有n個兩兩正交的單位特徵向量
定理2:在複數域上,A為正規矩陣的充分必要條件為A酉相似於對角矩陣
線上性代數中,三角矩陣是方形矩陣的一種,因其非零係數的排列呈三角形狀而得名。三角矩陣分上三角矩陣和下三角矩陣兩種。上三角矩陣的對角線左下方的係數全部為零...
分類 注意 特殊的三角矩陣 性質 推廣《矩陣論》是2013年清華大學出版社出版圖書。 本書比較全面、系統地介紹了矩陣的基本理論、方法及其套用。全書分上、下兩篇,共10章,分別介紹了線性空間與...
圖書信息 前言 目錄《矩陣理論及方法》是2012年科學出版社出版的圖書,作者是謝冬秀、雷紀剛、陳桂芝。
圖書信息 內容簡介 目錄矩陣分解 (decomposition, factorization)是將矩陣拆解為數個矩陣的乘積,可分為三角分解、滿秩分解、QR分解、Jordan分解...
QR分解法 奇異值分解法習題2.1 習題2.2 習題2.3
基本信息 內容介紹《矩陣理論與套用》是由科學出版社出版的圖書。
圖書信息 內容簡介 圖書目錄2-正規圖由不相連的圈組成。 3-正規圖稱為3次圖。 階為的正規圖是完全圖。
134§6.1正規矩陣134§6.2Hermite矩陣135一...矩陣論 ISBN: 978-7-5642-2793-7/F.2793...本書比較全面地介紹了矩陣理論的基礎知識。全書共分九章,分別介紹了線性空間...
