定義
如果一個矩陣與一個對角矩陣相似,我們就稱這個矩陣可經相似變換對角化,簡稱 可對角化;與之對應的線性變換就稱為 可對角化的線性變換。
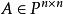 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣任取 ,則 可作為上n維線性空間V的某個線性變換 在一組基 下的矩陣。
 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣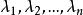 可對角化矩陣
可對角化矩陣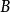 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣若 可對角化,即 使 成對角形,則B是 在另一組基 下的矩陣,且 ,記B的主對角線元素為 ,這是的全部特徵值,也是 的全部特徵值(因為兩矩陣相似),由線性變換的矩陣的定義知
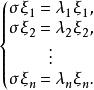 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣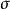 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣所以, 是 的n個線性無關的特徵向量,它們在基向量組 下的坐標 ,即T的列向量組,就是 的n個線性無關的特徵向量。
 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣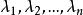 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣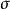 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣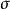 可對角化矩陣
可對角化矩陣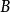 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣反過來,如果 有n個線性無關的特徵向量 ,與它們對應的特徵值是 ,以 為列向量組作成一個可逆矩陣T,令 ,就得到 的n個線性無關的特徵向量 ,用 作為V的基,則上述方程組成立,從而 在這組基下的矩陣是對角矩陣,並且 。
性質定理
定理1
 可對角化矩陣
可對角化矩陣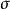 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣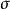 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣m級矩陣 或n維線性空間V的線性變換 可對角化的充要條件是或 有n個線性無關的特徵向量。當可對角化時,與它相似的對角矩陣的主對角線上的元素就是的全部特徵值。
 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣由上面的分析還知道,如果求出了矩陣的n個線性無關的特徵向量,那么用這些向量作列向量的矩陣T就使 成對角形,其主對角線上的元素就是的全部特徵值(按對應的特徵向量排序)。
定理2
屬於不同特徵值的特徵向量線性無關。
 可對角化矩陣
可對角化矩陣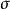 可對角化矩陣
可對角化矩陣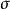 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣證明: 設 是線性變換 的m個不同的特徵值, 的屬於它們的特徵向量分別是 ,下面用數學歸納法證明 線性無關。
 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣(1)當 時,因為特徵向量 ,它一定線性無關。
 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣(2)假定 時, 線性無關。
 可對角化矩陣
可對角化矩陣當 時,令
 可對角化矩陣
可對角化矩陣①
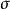 可對角化矩陣
可對角化矩陣用 對兩邊作用得
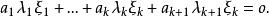 可對角化矩陣
可對角化矩陣②
 可對角化矩陣
可對角化矩陣①式兩邊乘以 得
 可對角化矩陣
可對角化矩陣③
從②減去③得
 可對角化矩陣
可對角化矩陣由歸納假設得
 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣因為 ,所以 ,將它們代入①得 ,於是 也線性無關。
 可對角化矩陣
可對角化矩陣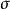 可對角化矩陣
可對角化矩陣用取代 的位置上述推理過程一樣正確,故定理得證。
在特徵值和特徵向量方面,矩陣與線性變換的理論是平行的,下面只就矩陣進行討論,所得的結果對線性變換也成立。
推論1
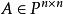 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣若 有n個不同的特徵值,則可對角化。
因為複數域上的n次多項式恰有n個根,所以我們還有下面的推論。
推論2
 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣如果的特徵多項式在複數域上的根互不相等,那么作為複數域上的矩陣一定可以對角化。
推論3
 可對角化矩陣
可對角化矩陣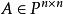 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣如果 是 的所有互不相同的特徵值,各特徵子空間 的基排列如下:
 可對角化矩陣
可對角化矩陣那么上述特徵向量組線性無關,從而特徵子空間的和是直和。
定理3
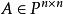 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣矩陣 可對角化的充要條件是 可以表為A的特徵子空間的直和。
 可對角化矩陣
可對角化矩陣證明: 若可對角化,根據定理1,它有n個線性無關的特徵向量,將它們按所屬的特徵值進行分組得到特徵向量組
 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣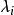 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣其中子組 中各向量同屬特徵值 ,它們一定是A的特徵子空間 的基(否則將不構成所在特徵子空間的基的各子組擴充成所在特徵子空間的基,由推論3知,A的線性無關的特徵向量的個數大於n,這與 矛盾),於是
 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣反過來,設 ,從各個特徵子空間取出一組基就得到的n個線性無關的特徵向量,故可對角化。
定理4
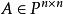 可對角化矩陣
可對角化矩陣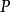 可對角化矩陣
可對角化矩陣矩陣 可對角化的充要條件是A的特徵多項式在上可以分解為
 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣 可對角化矩陣
可對角化矩陣的形式,並且特徵子空間 的維數 。

