定義
 特徵多項式
特徵多項式 特徵多項式
特徵多項式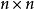 特徵多項式
特徵多項式 特徵多項式
特徵多項式設為域(例如實數或複數域),對布於上的矩陣,定義其 特徵多項式為
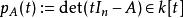 特徵多項式
特徵多項式這是一個n次多項式,其首項係數為一。
一般而言,對布於任何交換環上的方陣都能定義特徵多項式。
要理解特徵多項式,首先需要了解一下特徵值與特徵向量,這些都是聯繫在一起的:
設A是n階矩陣,如果數λ和n維非零列向量x使得關係式Ax=λx成立,那么,這樣的數λ就稱為方陣A的特徵值,非零向量x稱為A對應於特徵值λ的特徵向量。
然後,我們也就可以對關係式進行變換:(A-λE)x=0 其中E為單位矩陣。這是n個未知數n個方程的齊次線性方程組,它有非零解的充要條件是係數行列式為0,即|A-λE|=0。帶入具體的數字或者符號,可以看出該式是以λ為未知數的一元n次方程,稱為方陣A的特徵方程,左端 |A-λE|是λ的n次多項式,也稱為方陣A的特徵多項式。
解法
1、把|λE-A|的各行(或各列)加起來,若相等,則把相等的部分提出來(一次因式)後,剩下的部分是二次多項式,肯定可以分解因式。
2、把|λE-A|的某一行(或某一列)中不含λ的兩個元素之一化為零,往往會出現公因子,提出來,剩下的又是一二次多項式。
3、試根法分解因式。
性質
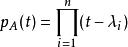 特徵多項式
特徵多項式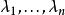 特徵多項式
特徵多項式當A為上三角矩陣(或下三角矩陣)時,,其中是主對角線上的元素。
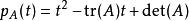 特徵多項式
特徵多項式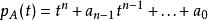 特徵多項式
特徵多項式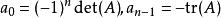 特徵多項式
特徵多項式對於二階方陣,特徵多項式能表為。一般而言,若,則。
此外:
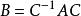 特徵多項式
特徵多項式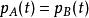 特徵多項式
特徵多項式(1)特徵多項式在基變更下不變:若存在可逆方陣 C使得,則。
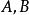 特徵多項式
特徵多項式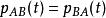 特徵多項式
特徵多項式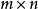 特徵多項式
特徵多項式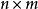 特徵多項式
特徵多項式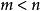 特徵多項式
特徵多項式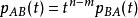 特徵多項式
特徵多項式(2)對任意兩方陣,有。一般而言,若A為矩陣,B 為矩陣(設),則。
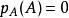 特徵多項式
特徵多項式(3)凱萊-哈密頓定理:。

