逆矩陣

逆矩陣（英語：inverse matrix）是一種計算方法。設A是數域上的一個n階方陣，若在相同數域上存在另一個n階矩陣B，使得： AB=BA=E。則稱B是A的逆矩陣，而A則被稱為可逆矩陣。

基本信息

• 中文名：逆矩陣

• 定義：設A是數域上的一個n階方陣，若在相同數域上存在另一個n階矩陣B，使得： AB=BA=E。 則我們稱B是A的逆矩陣，
• 可逆條件：A是可逆矩陣的充分必要條件是∣A∣≠0，即可逆矩陣就是非奇異矩陣。（當∣A∣=0時，A稱為奇異矩陣）
• 套用：數學

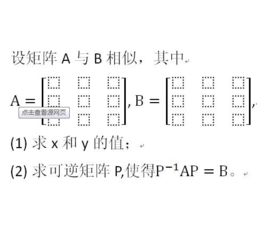
矩陣可逆的條件

A是可逆矩陣的充分必要條件是∣A∣≠0，即可逆矩陣就是非奇異矩陣。（當∣A∣=0時，A稱為奇異矩陣）

matlab中的求法

inv(a)或a^-1。

例如：

>> a =

8 4 9

2 3 5

7 6 1

>> a^-1

ans =

0.1636 -0.3030 0.0424

-0.2000 0.3333 0.1333

0.0545 0.1212 -0.0970

>> inv(a)

ans =

0.1636 -0.3030 0.0424

-0.2000 0.3333 0.1333

0.0545 0.1212 -0.0970

以下是對MATLAB中Inv用法的解釋。

原文（來自matlab help doc）

In practice, it is seldom necessary to form the explicit inverse of a matrix. A frequent misuse of inv

arises when solving the system of linear equations A

=B .

One way to solve this is with x = inv(A)*B.A better way, from both an execution time and numerical accuracy standpoint,is to use the matrix division operator x = A\b.

實際上，很少需要矩陣逆的精確值。在解方程 A

=B的時候可以使用x = inv(A)*B，

但通常我們求解這種形式的線性方程時，不必要求出A的逆 矩陣，在MATLAB中精度更高，速度更快的方法是用左除——x = A\b。

另外，用LU分解法的速度更快，只是要多寫一條LU分解語句。

速度可以通過matlab中tic和toc來估算運行的時間。