定義
對角矩陣(diagonal matrix)是一個主對角線之外的元素皆為0的矩陣。對角線上的元素可以為0或其他值。對角線上元素相等的對角矩陣稱為數量矩陣;對角線上元素全為1的對角矩陣稱為單位矩陣。
(1)對角矩陣形如:
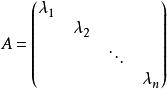 對角矩陣
對角矩陣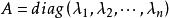 對角矩陣
對角矩陣(2)對角矩陣可以記作:。
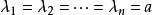 對角矩陣
對角矩陣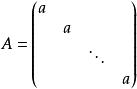 對角矩陣
對角矩陣(3)當時,對角陣稱為數量矩陣。
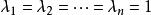 對角矩陣
對角矩陣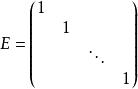 對角矩陣
對角矩陣(4)當時,叫做單位矩陣,記作E,有。
運算規律
和差運算
同階對角陣的和、差仍是對角陣,有:
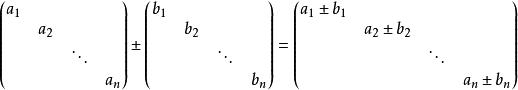 對角矩陣
對角矩陣數乘運算
數與對角陣的乘積仍為對角陣,有:
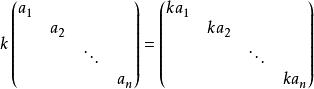 對角矩陣
對角矩陣乘積運算
同階對角矩陣的乘積仍為對角陣,且它們的乘積是可交換的,有:
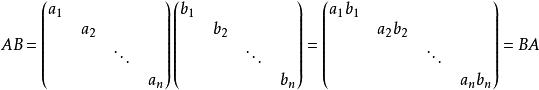 對角矩陣
對角矩陣矩陣條件
充要條件
n階矩陣A相似於對角矩陣的充要條件是A有n個線性無關的特徵向量。
證明過程:
(1)必要性。
設有可逆矩陣P,使得
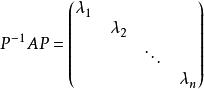 對角矩陣
對角矩陣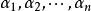 對角矩陣
對角矩陣令矩陣P的n個列向量為,則有
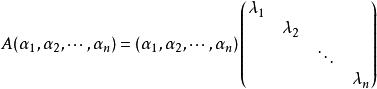 對角矩陣
對角矩陣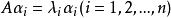 對角矩陣
對角矩陣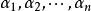 對角矩陣
對角矩陣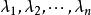 對角矩陣
對角矩陣因而,因為P為可逆矩陣,所以為線性無關的非零向量,它們分別是矩陣A對應於特徵值的特徵向量。
(2)充分性。
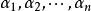 對角矩陣
對角矩陣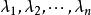 對角矩陣
對角矩陣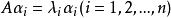 對角矩陣
對角矩陣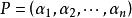 對角矩陣
對角矩陣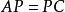 對角矩陣
對角矩陣由必要性的證明可見,如果矩陣A有n個線性無關的特徵向量,設它們為,對應的特徵值分別為,則有,以這些向量為列構造矩陣,則P可逆,且,其中C如下:
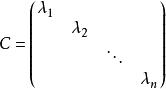 對角矩陣
對角矩陣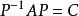 對角矩陣
對角矩陣即。
推論
若n階矩陣A有n個不同的特徵值,則A必能相似於對角矩陣。
說明:當A的特徵方程有重根時.就不一定有n個線性無關的特徵向量,從而未必能對角化。

