實對稱矩陣

基本信息

• 中文名：實對稱矩陣
• 英文名：symmetric matrices

• 定義：元素都為實數，矩陣轉置等於本身
• 特徵：特徵值為實數，特徵向量為實向量

簡介

如果有n階矩陣A，其各個元素都為實數，矩陣A的轉置等於其本身(AT=A)，則稱A為實對稱矩陣。如果有n階矩陣A，其各個元素都為實數，且aij=aji；i，j=1，2，...，n（即這裡T表示轉置），則稱A為實對稱矩陣。

主要性質

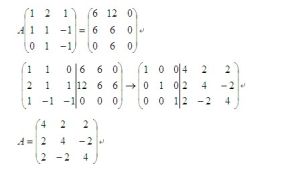實對稱矩陣

1.實對稱矩陣A的不同特徵值所對應的特徵向量是正交的。2.實對稱矩陣A的特徵值都是實數，特徵向量都是實向量。
3.n階實對稱矩陣A必可對角化。
4.可用正交矩陣對角化。
5.K重特徵值必有K個線性無關的特徵向量，或者說必有秩r(λE-A)=n-k。
6.實對稱陣可相似對角化，且相似對角陣上的元素即矩陣本身特徵值。