酉矩陣

n階複方陣U的n個列向量是U空間的一個標準正交基，則U是酉矩陣(Unitary Matrix)。顯然酉矩陣是正交矩陣往複數域上的推廣。 酉矩陣又稱為么正矩陣。在2000年之前的很多國內教材（特別是老版本教材）中用“么正矩陣”名稱的比較多。需要注意的是，么正矩陣和麼模正交矩陣是兩個不同的概念。 為了將概念延伸到復域即新的酉空間中提出了酉矩陣。

基本信息

• 中文名：酉矩陣
• 其他外文名：Unitary Matrix
• 別稱：么正矩陣
• 定義：若一行列的複數矩陣滿足：其中，為的共軛轉置，為階單位矩陣，則稱為酉矩陣。
• 類型：數學術語
• 符號：U

• 判別準則：酉矩陣共軛轉置和其逆矩陣相等
• 一級學科：數學
• 二級學科：矩陣

定義

酉矩陣

酉矩陣

酉矩陣

若一 行 列的複數矩陣 滿足：

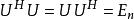酉矩陣

酉矩陣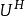

酉矩陣

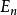酉矩陣

酉矩陣

酉矩陣

其中， 為 的共軛轉置， 為 階單位矩陣，則 稱為酉矩陣。

判別準則

一個簡單的充分必要判別準則是：

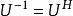酉矩陣

或者說，酉矩陣的共軛轉置和它的逆矩陣相等。

性質和套用

酉矩陣的相關性質：

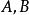酉矩陣

設有矩陣 ，則

酉矩陣

酉矩陣

（1）若 是酉矩陣，則 的逆矩陣也是酉矩陣；

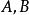酉矩陣

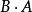酉矩陣

酉矩陣

（2）若 是酉矩陣，則 和也是酉矩陣；

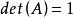酉矩陣

酉矩陣

（3）若 是酉矩陣，則 ；

酉矩陣

酉矩陣

（4） 是酉矩陣的充分必要條件是，它的 個列向量是兩兩正交的單位向量。

酉方陣在量子力學中有著重要的套用。酉等價是標準正交基到標準正交基的特殊基變換。

廣義酉矩陣

定義

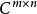酉矩陣

酉矩陣

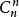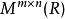酉矩陣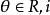

酉矩陣

酉矩陣

假定表示所有m×n復矩陣的集合，表示所有n階復可逆矩陣的集合，表示所有m×n實矩陣的集合，，（表示純虛數）。

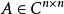酉矩陣

酉矩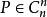陣

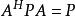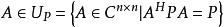酉矩陣

酉矩陣

定義1，設，若存在使，則稱A為n階P-廣義酉矩陣；記為。

性質

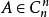酉矩陣

定理1，若相似於一個酉矩陣U，則A是n階P-廣義酉矩陣。

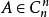酉矩陣

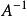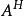酉矩陣

酉矩陣

推論1，若相似於一個酉矩陣U，則與相似。

定理2，已知A可對角化，則A為n階P-廣義酉矩陣的充分必要條件是A相似於一個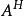酉矩陣。

酉矩陣

定理3，已知A是n階P-廣義酉矩陣。如果λ≠0是A的特徵值，那么1/λ是的特徵值；當A為實矩陣時，1/λ也是A的特徵值。

定理4，若A為廣義P-酉矩陣，則A是廣義P -酉矩陣。