水中能見度
正文
水中視程。能見度是從大氣光學借用來的術語。水中能見度比大氣中的能見度低得多。海水中的水平視程通常為大氣中視程的千分之一左右,主要原因是光在海水中的衰減和散射比在大氣中強烈得多。水中目標的識別,取決於目標與背景之間的輻亮度和顏色的差別。隨觀察距離增大,水中的目標與背景的輻亮度的差別迅速減少,目標物變得更加模糊。由於水中能見度理論主要解決圖象在水中傳輸的問題,因此海水的對比度和光學傳遞函式,都是主要的研究內容。對比度 若目標的輻亮度為 L0,背景輻亮度為Lb0,則目標相對於背景的固有對比度c0為
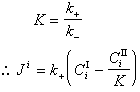
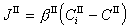 。
。
早在1948年,美國斯克里普斯海洋研究所能見度實驗室用玻璃底殼船在海上進行了觀測實驗。當垂直向下觀察時,發現cr與c0之比隨著觀察距離r 的增加而按指數律衰減,可表示為Cr=C0exp(-0.810r)。式中0.810為海水的對比度衰減係數。實驗測得的海水線性衰減係數 μ為0.594,輻照度衰減係數k 為0.216。μ與k之和恰等於對比度衰減係數。因此,Cr=C0exp[-(μ+k)r]。當觀察方向偏離垂直方向時, 實驗還發現 Cr=C0exp[-(μ+kcosθ)r],式中 θ為觀察方向與天頂方向之間的夾角,這就是對比度傳輸和海洋光學參數的經驗關係。 自海洋輻射傳遞方程出發, 假定光在均勻水體中傳播的條件下,從理論上也證明了這個關係式。根據對比度傳輸規律,當表現對比度下降 1/e時,觀察距離l=1/(μ+kcosθ),稱l為對比度衰減長度。清潔的海水的對比度衰減長度可達20米左右,海岸帶水體的對比度衰減長度約為5米,混濁水體的對比度衰減長度有時只有幾厘米。人眼所能觀察到的對比度的下限為0.02,黑色目標在自然光照條件下的水平觀察視程為 4個衰減長度,而大多數目標的視程為黑色目標視程的 7/8。在夜晚無自然光照條件下,自身發光的目標的視程,在理論上可達無窮大,但實際上只能達到15~20個衰減長度。
圖像在水中的傳輸 海洋光學中用海水的光學傳遞函式 (OTF)來表征圖像通過海水後的模糊程度。若目標為理想點源s(x,у),通過海洋水體傳輸後,在理想成像系統所成的像為h(θ,r),則h(θ,r)稱為海洋水體的點擴展函式,h(θ,r)的傅立葉變換H (ψ,r)則定義為海洋水體的光學傳遞函式,其中ψ為圖像的空間角頻率單位為周/弧度(c/rad),光學傳遞函式的模|H (ψ),r)|稱為調製傳遞函式(MTF)。顯然,海水的散射越強,h(θ,r)的有效半徑越大,圖像解析度的損失越大,從而使圖像的高頻成分或圖像的細微結構發生模糊。海水的點擴展函式或海水的光學傳遞函式,都是衡量水中圖像傳輸質量的最佳的客觀標準。光學傳遞函式隨著距離r 的增加而按指數率衰減,一般表示為
H(ψ,r)=exp【-D(ψ)·r】D(ψ)
為空間角頻率衰減函式,其值隨ψ的增大而增大。點擴展函式為H(ψ),r)的傅立葉變換。顯然,測定通過路徑r的海水小角度光散射,即可測得 h(θ,r),由此可推出海洋水體的光學傳遞函式H(ψ,r)。還有一種用光學傳遞函式儀測定H(ψ,r)的方法,其原理是用空間頻率調製模板來接收空間頻率信號,以確定通過水中路徑之後圖像空間角頻率的衰減程度。圖為測得的典型的沿岸清潔海水的空間角頻率衰減函式D(ψ)。由圖可見,高頻的衰減長度為7米,而低頻的衰減長度為30米。 參考書目N.G.Je rlov,ed.,OpticalAspects Of Oceanog-raphy,Academic Press,New York,1974.
