定義
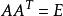 正交陣
正交陣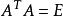 正交陣
正交陣若n階方陣A滿足或者,則稱A為正交陣,其中E為n階單位陣。
性質
設A是n階正交陣,則
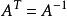 正交陣
正交陣(1);
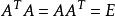 正交陣
正交陣(2)(E是n階單位陣);
 正交陣
正交陣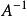 正交陣
正交陣(3)若A是正交陣,則或亦是正交陣;
(4)若A、B是正交陣,則AB亦是正交陣;
(5)|A|=1或|A|=-1;
(6)實對稱陣的對應不同特徵值的特徵向量正交。
(7)若A是正交陣,則λ=±1
充要條件
方陣A為正交陣的充分必要條件是A的行向量或列向量是標準正交向量。

正交陣是指滿足AA^T=E或者A^T A=E的n階方陣A,其中E為n階單位陣。
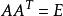 正交陣
正交陣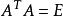 正交陣
正交陣若n階方陣A滿足或者,則稱A為正交陣,其中E為n階單位陣。
設A是n階正交陣,則
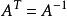 正交陣
正交陣(1);
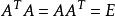 正交陣
正交陣(2)(E是n階單位陣);
 正交陣
正交陣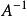 正交陣
正交陣(3)若A是正交陣,則或亦是正交陣;
(4)若A、B是正交陣,則AB亦是正交陣;
(5)|A|=1或|A|=-1;
(6)實對稱陣的對應不同特徵值的特徵向量正交。
(7)若A是正交陣,則λ=±1
方陣A為正交陣的充分必要條件是A的行向量或列向量是標準正交向量。
“正交性”是從幾何中借來的術語。如果兩條直線相交成直角,他們就是正交的。用向量術語來說,這兩條直線互不依賴。沿著某一條直線移動,該直線投影到另一條直線上...
定義 相關概念 正交化方法在組合數學中,擬陣是一個對向量空間中線性獨立概念的概括與歸納的數學結構。擬陣有許多等價的定義方式,最常見的定義方式是用獨立集,基,圈,閉集合,閉平面,閉...
來源 有限擬陣定義 樣例 基本構造 相關術語如果AA=E(E為單位矩陣,A表示“矩陣A的轉置矩陣”)或AA=E,則n階實矩陣A稱為正交矩陣 。正交矩陣是實數特殊化的酉矩陣,因此總是屬於正規矩陣。盡...
定義 定理 舉例 基本構造 基本特性本書介紹了基於無人水下航行器舷側陣的多目標探測技術,主要分為基於合成孔徑技術的多目標探測技術和基於多輸入多輸出陣列處理技術的多目標探測技術兩大部分。全書...
內容簡介 作者簡介 圖書目錄 序言的元素能使V取得極大值 [3] 。方差極大的正交旋轉記因子載荷陣為...。所謂方差極大的正交旋轉,即選擇正交陣,使達最大。當m=2時,正交陣可表...矩陣P(P非正交陣),使AP的總方差達最大的變換稱為方差極大的斜交旋轉...
基本介紹 詳細說明 方差極大的正交旋轉 方差極大的斜交旋轉。 雅可比方法 對稱矩陣可以通過正交相似變換化為對角陣,其對角元是原矩陣...。 變換方法是利用一系列特殊的變換矩陣(初等下三角陣、豪斯霍爾德矩陣、平面旋轉...特徵值的特殊形式的矩陣(對角陣、三角陣、擬三角陣等);多用於求解全部特徵值...
正文 配圖 相關連線,又(gij)仍構成正定對稱陣,那么從出發,也可以定義一種幾何學,這便是黎曼幾何學...,…,xn+dxn)之間的距離。這裡(gij)構成一個正定對稱的n×n陣,並假設...,即,就稱X、Y 為互相正交。│尣│=1的向量稱為單位向量,Tp(M)中...
黎曼幾何學 正文 配圖 相關連線σ是n維酉空間V的酉變換,則存在V的標準正交基,使σ關於此基的矩陣為對角形...正交基的矩陣是酉矩陣(酉變換(或正交變換)在標準正交基下的矩陣表示是酉矩陣(或正交矩陣));4.若ε,ε,…,ε是V的標準正交基...
基本介紹 相關結論 相關概念Hermite陣。顯然,Hermite陣主對角線上的元素必須是實數。對於只包含實數元素的矩陣(實矩陣),如果它是對稱陣,即所有元素關於主對角線對稱,那么它也是Hermite陣。也就是說,實對稱陣是Hermite陣的特例...
基本信息 性質 序列