酉變換

酉變換(unitary transformation)是指酉空間V的等度量變換。對∀α，β∈V，滿足條件(σ(α)，σ(β))=(α，β)的線性變換σ稱為酉變換。對n維酉空間V的每一酉變換σ，都存在V的標準正交基，使σ關於此基的矩陣為對角形，且對角線上元素的模為1。以下陳述都是線性變換σ為酉變換的充分必要條件：1.對酉空間的每一向量α，|σ(α)|=|α|；2.σ關於某一組標準正交基的矩陣是酉矩陣；3.若ε1，ε2，…，εn是標準正交基，則σ(ε1)，σ(ε2)，…，σ(εn)也是標準正交基 。酉變換是不變內積的變換，在歐氏空間中則稱為正交變換。

基本介紹

酉變換是一種線性變換。設σ是酉空間V的線性變換，若對任意的α，β∈V，(σ(α)，σ(β))=(α，β)，則稱σ為V上的酉變換。設σ是n維酉空間V的酉變換，則存在V的標準正交基，使σ關於此基的矩陣為對角形，且對角線上元素的模為1。設σ是n維酉空間V的線性變換，則下列命題等價：

1.σ是酉變換；

2.|σ(α)|=|α|，對任意的α∈V；

3.σ關於標準正交基的矩陣是酉矩陣（酉變換(或正交變換)在標準正交基下的矩陣表示是酉矩陣(或正交矩陣)）；

4.若ε，ε，…，ε是V的標準正交基，則σ(ε)，σ(ε)，…，σ(ε)也是V的標準正交基 。

相關結論

定理1 設V為酉空間，則

酉變換

A為V的酉變換A把V的規範正交基仍變為規範正交基 。

定理2 設V為酉空間，則

酉變換

A為V的酉變換A關於V的任一個規範正交基的矩陣是酉矩陣。

在酉空間裡，同樣有對稱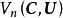變換。

酉變換

定理3的酉變換是線性變換 。

相關概念

對稱變換

定義 設V為酉空間，A∈L(V)，如果

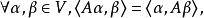酉變換

則稱線性變換A為V的 對稱變換 。

對於對稱變換，我們有下面的結論。

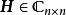酉變換

定義 設，如果

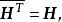酉變換

對稱矩陣 H為埃爾米特(Hermite)矩陣。

定理 設V為酉空問，則

酉變換

A為V的對稱變換A關於V的任一個規範正交基的矩陣是埃爾米特矩陣。

關於對稱變換與埃爾米特矩陣還有下面的結論。

定理 設V為酉空間，A為V的對稱變換，則

(1)A的特徵值是實數；

(2)A的屬於不同特徵值的特徵向量正交；

(3)存在V的一個規範正交基，使得A關於這個基的矩陣是對角矩陣。

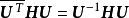酉變換

定理 設 H是為n階埃爾米特矩陣，則存在n階酉矩陣 U，使得是一個對角矩陣。

ie：埃爾米特矩陣一定“酉相似”於一個對角矩陣 。

Household變換

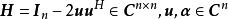酉變換

酉變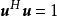換

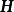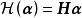酉變換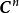

酉變換

酉變換

設，且。則由矩陣所確定的線性變換是中的酉變換。

Household矩陣有以下性質：

①；(Hermite矩陣)

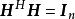酉變換

②；(酉矩陣)

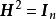酉變換

③；(對合陣)

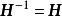酉變換

④；(自逆陣)

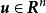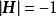酉變換

酉變換

⑤若，則。

Household變換也稱為初等反射變換，而Household矩陣也稱為初等反射矩陣 。