代數特徵值問題數值解法

對元素為實數或複數的 n×n矩陣A，求數λ和n維非零向量 x使Ax=λx，這樣的問題稱為代數特徵值問題,也稱矩陣特徵值問題，λ和 x分別稱為矩陣A的特徵值和特徵向量。

正文

　代數特徵值問題的數值解法是計算數學的主要研究課題之一，它常出現於動力系統和結構系統的振動問題中。在常微分方程和偏微分方程的數值分析中確定連續問題的近似特徵系，若用有限元方法或有限差分方法求解，最終也化成代數特徵值問題。此外，其他數值方法的理論分析，例如確定某些疊代法的收斂性條件和初值問題差分法的穩定性條件，以及討論計算過程對捨入誤差的穩定性問題等都與特徵值問題有密切聯繫。求解矩陣特徵值問題已有不少有效而可靠的方法。
矩陣A的特徵值是它的特徵多項式Pn(λ)呏det(λI-A)的根, 其中I為單位矩陣。但階數超過4的多項式一般不能用有限次運算求出根，因而特徵值問題的計算方法本質上是疊代性質的，基本上可分為向量疊代法和變換方法兩類。
向量疊代法是不破壞原矩陣A，而利用A對某些向量作運算產生疊代向量的求解方法，多用來求矩陣的部分極端特徵值和相應的特徵向量，特別適用於高階稀疏矩陣。乘冪法、反冪法都屬此類，隆措什方法也常作為疊代法使用。
變換方法是利用一系列特殊的變換矩陣（初等下三角陣、豪斯霍爾德矩陣、平面鏇轉矩陣等）,從矩陣A出發逐次進行相似變換，使變換後的矩陣序列趨於容易求得特徵值的特殊形式的矩陣（對角陣、三角陣、擬三角陣等）；多用於求解全部特徵值問題，其優點是收斂速度快，計算結果可靠，但由於原矩陣A被破壞，當A是稀疏矩陣時，在計算過程中很難保持它的稀疏性，因而大多數變換方法只適於求解中小規模稠密矩陣的全部特徵值問題。雅可比方法、吉文斯－豪斯霍爾德方法以及LR方法、QR方法等都屬此類。
乘冪法　計算矩陣的按模最大的特徵值及對應特徵向量的一種向量疊代法。設 A為具有線性初等因子的矩陣，它的n 個線性無關的特徵向量是ui(i=1,2,…,n)，特徵值排列次序滿足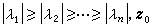是一個n維非零向量,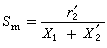於是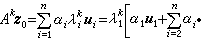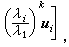若│λ1│>│λ2│, 則當α1≠0,且k足夠大時，Akz0除相差一個純量因子外趨於λ1所對應的特徵向量，這就是乘冪法的基本思想。實際計算中最簡單情況的乘冪法的疊代格式是：取初始向量z0，計算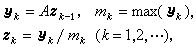

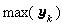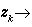
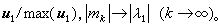式中指中絕對值最大的一個分量,這時 一般情形下，由於計算格式依賴於A的特徵值的分布情況,實際使用很不方便，只是在求階數非常高的矩陣的個別特徵值和相應的特徵向量時偶爾使用。然而乘冪法的基本思想是重要的，由它可導出許多實用的計算方法，例如反冪法和子空間疊代法,它也是其他一些有效計算方法（例如LR方法,QR方法）的理論基礎。
子空間疊代法　又稱同時疊代法，乘冪法的直接推廣，能同時求出模最大的一些特徵值和相應的特徵向量。它與乘冪法的差別主要在二個方面：①同時用p(p>1)個正交規範向量進行類似於乘冪法的疊代，將疊代向量看作一個p 維子空間的正交規範基，每次疊代後得到一個新的子空間；②疊代過程中，在p 維子空間上套用里茨原理進行加速。這個方法更便於使用計算機自動計算，而且加快了收斂速度，是大型稀疏矩陣特徵值問題的有效解法。
反冪法　又稱反疊代,其原理是:設矩陣A非奇異,為求 A的模最小的特徵值和相應的特徵向量而對A-1使用乘冪法。A-1的特徵值次序是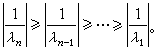取z0為初始向量，疊代格式為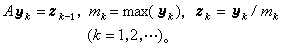

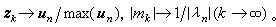在一定條件下反冪法的每次疊代要解一個線代數方程組。這種原始的反冪法在實際計算中很少套用，實際使用的反冪法總是帶原點位移的，且位移常取為已求得的近似特徵值，而用反冪法求其對應的特徵向量。設慞i是 A的某特徵值λi的近似值，帶原點位移慞i的反冪法的疊代格式是：取初始向量z0，計算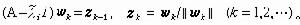

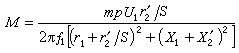當 時, 按方向收斂於特徵向量ui，收斂商是慞i越精確,收斂就越快，但就越接近奇異矩陣,因而在疊代過程中需要求解非常病態的方程組。然而已經證明，這個病態性質對於反冪法的按方向收斂於特徵向量是無關緊要的，而且當慞i相當精確時，一般只要一、二次反疊代就可求得相當精確的近似特徵向量。反冪法是由已知近似特徵值求對應近似特徵向量的有效方法。
隆措什方法　 用相似變換將矩陣 A 約化為三對角矩陣的一種方法，其特點是不破壞原矩陣A 。目前能實際使用的是 A對稱時的對稱隆措什方法：取初始向量v1，‖v1‖=1，遞推地計算　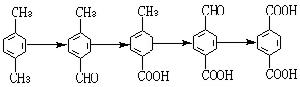 式中 αi和βi由使｛vi｝為正交規範化的條件確定，即 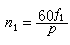當精確計算時vn+1=0，上述過程可寫成矩陣形式 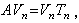其中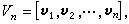Tn是對稱三對角矩陣

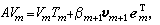它的特徵值可由二分法求得。由於捨入誤差的影響,隆措什方法所產生的隆措什向量很快失去正交性，因而這方法長期來被認為不穩定,很少用於實際計算。近年來對隆措什方法作了深入研究，進行了大量實際計算和細緻的誤差分析,並且觀察到如下的所謂隆措什現象：將m步遞推關係寫為其中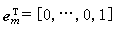是m維行向量。對足夠大的m,矩陣Tm的特徵值包括A的所有相異特徵值。注意,當出現捨入誤差時，可能m>n。對高階矩陣A,對不大的m(m<<n),Tm常包含A的相當精確的近似特徵值。由於隆措什方法的這一特性，還由於該方法能保持A的稀疏性,所以目前它已成為求高階對稱稀疏矩陣部分特徵值的最有效方法。
雅可比方法　對稱矩陣可以通過正交相似變換化為對角陣,其對角元是原矩陣的全部特徵值。雅可比方法就是通過一系列特殊的正交相似變換──雅可比鏇轉，使對稱矩陣近似對角化從而求得特徵值和特徵向量的方法。記A0=A,作正交相似序列其中Rk是(p,q)超平面的雅可比鏇轉矩陣，即

p、q的選取應使中非對角元絕對值最大者。Ak和Ak-1僅在第p 行(列)和第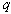行(列)不同,它們之間的關係為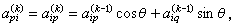

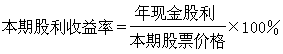
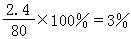
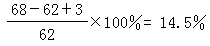
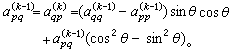
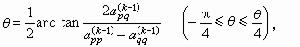
選

可使

當k →時,AK趨於對角陣,這就是經典雅可比方法。此方法在第k次變換前要搜尋Ak-1的非對角元中絕對值最大者以確定雅可比鏇轉矩陣的鏇轉平面，但這很費時間。為避免這種消耗,可改用循環雅可比方法:在n(n-1)/2次的相繼雅可比鏇轉(稱為一次掃描)中,每個非對角元,不管按什麼次序，恰好消去一次。其中最方便的是特殊循環雅可比方法，即每次掃描都按(1,2)，(1,3)，…，(1,n)；(2,3)，…，(2,n)；…；(n-1,n)的次序進行。實際計算中最廣泛使用的是特殊循環雅可比方法的一種變形，稱為閾雅可比方法：確定一個正數作閾值，在特殊循環的一次掃描中只對絕對值超過閾值的非對角元所在的平面進行鏇轉變換，反覆掃描，當所有非對角元的絕對值都不超過閾值時減小閾值，再按新的閾值進行掃描，如此繼續下去，直至閾值充分小而達到近似對角化。雅可比方法的優點是：能在求特徵值的同時求得相當精確的近似正交規範特徵向量系；缺點是：與其他變換方法相比，收斂速度較慢。它適用於求解低階稠密矩陣的全部特徵值問題，對近似對角（即非對角元素較小）的對稱矩陣特別有效，常套用於子空間疊代法的里茨加速過程中。
吉文斯-豪斯霍爾德方法　一種計算對稱矩陣A的全部或部分特徵值及對應特徵向量的方法，包括下述三個主要部分:①利用豪斯霍爾德變換(正交相似變換)將A化為對稱三對角矩陣C，整個過程由n-2步組成,第r步的變換矩陣是 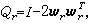其中記A0=A，當Ar-1的第r階順序主子矩陣已是三對角形時,第r步將Ar-1變換為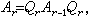使Ar的第r+1階順序主子矩陣是三對角的。經n-2步變換後，得到對稱三對角矩陣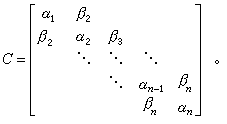

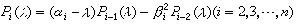法計算C 的特徵值。當βi≠0（i=2,3,…，n）時,由C-λI 的順序主子式組成的多項式序列P0(λ)呏1，P1=α1-λ，構成一個斯圖姆序列。用α（α）表示P0(α)，P1(α),…,Pn(α)中相鄰二數符號一致的數目，它就是 Pn（λ）在【α，)中根的個數。設C 的特徵值是λ1>λ2>…>λn,而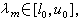且α(l0)≥m,α(u0)≤r>m 。用二等分［l0，u0］，計算α（r1）。若α（r1）≥m，則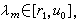取l1=r1,u1=u0；否則取l1=l0,u1=r1。因此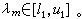繼續進行這樣的二分過程,就可求得λm的近似值。③套用帶近似特徵值位移的反冪法求C 的對應特徵向量,再利用①中的變換矩陣Q1,Q2,…,Qn-2 求得A的對應特徵向量。吉文斯-豪斯霍爾德方法速度快,計算過程穩定,一般說來優於雅可比方法,但它也要破壞原矩陣，因而適用於求解中小型矩陣的特徵值問題。
LR方法　原理及基本算法如下：當A的前n-1個順序主子式不為零時，可將A分解為A=LR，其中L是單位下三角陣,R 是上三角陣。記A1=A,進行疊代循環:作AK的LR分解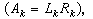計算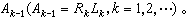由此得矩陣序列{AK}，每個AK都與A相似：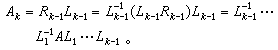

件下，AK→R(k→)，其中R 是上三角陣，其對角元是 A的全部特徵值。實際計算中為加快收斂速度常引進原點位移，記第k次疊代的原點位移為sK,帶原點位移的LR算法是: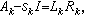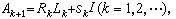所得矩陣序列{AK}中的每個矩陣也都與A相似,sK常取為AK的右下角元素。LR方法主要用於求解復矩陣的特徵值問題，其優點是計算量少，收斂速度快，缺點是計算穩定性差，適用範圍較小。求得近似特徵值後，常用帶位移的反冪法求對應特徵向量。
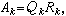
QR方法　求矩陣特徵值的最有效方法之一，是LR方法的酉類似，基本算法如下：作A的分解A=QR，其中Q是酉矩陣,R 是上三角陣。記A1=A,進行疊代循環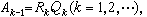矩陣序列{AK}中每一矩陣都與A相似: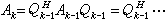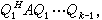QH表示矩陣Q的共軛轉置矩陣。在一定條件下Ak趨於上三角陣，但其上三角部分的元素不一定有極限，這樣的收斂稱為基本收斂，這對求特徵值來說已足夠，因為基本收斂的“極限矩陣”的對角元是A 的全部特徵值。每次疊代需作一次QR分解和一次矩陣乘法。為減少計算量,總是先將A經酉相似變換化為上黑森貝格矩陣H，再對H 套用 QR算法,上黑森貝格矩陣經QR疊代仍保持上黑森貝格形。為加速QR過程的收斂，常引進原點位移，它和帶位移的LR算法完全類似, 第k步的位移sk常取為Ak的右下角元素 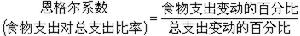，或右下角二階矩陣的特徵值中最接近 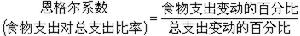者。帶原點位移的QR算法的漸近收斂速度至少是2次,當A對稱時可達3次。對實矩陣A，當A有復共軛特徵值時帶實原點位移的QR算法不可能收斂，為此發展了對實矩陣的雙重步QR算法，其基本思想是將可能帶復原點位移的QR算法中的相繼二步合併成一個雙重步以避免復運算。當求得近似特徵值後，可用帶位移的反冪法求對應的特徵向量。
病態特徵值問題　對特徵值問題Ax＝λx,設A的元素經小的擾動ΔA（即‖ΔA‖/‖A‖很小）變為A+ΔA，特徵值λ（假定是單的）和特徵向量 x相應地變為λ＋Δλ和x＋Δx，若｜Δλ｜/‖ΔA‖(或‖Δx‖/‖ΔA‖)非常大,則稱特徵值 λ（或特徵向量x）是病態的,否則稱為良態的。病態與否是特徵值問題的固有性質，與用何種方法進行數值求解無關。然而,誤差分析理論指出,受原始數據在計算機中表示的捨入誤差和數值方法求解過程中捨入誤差的影響而求得的對 A的特徵值問題的近似解，等於對A+ΔA的特徵值問題的精確解，這裡ΔA是一族依賴於數值方法的擾動矩陣。穩定的數值方法能保證‖ΔA‖/‖A‖是小的，但不能使病態問題變成良態的。求解病態特徵值問題是近年發展起來的矩陣不變子空間計算的重要內容。
廣義特徵值問題數值解法　最一般的矩陣特徵值問題是非線性的。 設T(λ)是 n×n 矩陣，其元素是λ的解析函式，確定數λ和非零向量x，使 T（λ）x＝0，這稱為非線性特徵值問題, λ是特徵值，x是相應的特徵向量。一種重要的特殊情況是一次廣義特徵值問題：A和B是n×n矩陣，求數λ和非零向量x，使 Ax＝λBx，B=I時就是通常特徵值問題；較一般的是 r次廣義特徵值問題:Ai（i=1,2,…,r）是n×n矩陣, 求數λ和非零向量x,使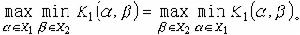。令x(0)=x,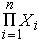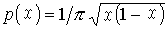r次廣義特徵值問題即可化為一次廣義特徵值問題：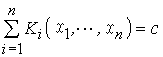

的非線性特徵值問題，當用線性化方法求解時，最終也歸為求解一系列一次廣義特徵值問題。對於一次廣義特徵值問題Ax＝λBx，當B非奇異時,可化為通常特徵值問題(B-1A)x=λx，當A、B對稱，且B正定時,可化為對稱特徵值問題(U -TAU-1)(Ux)＝λ(Ux)，其中U是B 的喬萊斯基分解B＝U TU中的上三角陣。利用化為通常特徵值問題來求解一次廣義特徵值問題有時是很有效的，但有下列缺點：①當A和B是稀疏矩陣，特別是帶形矩陣時，約化後的矩陣B-1A或 U -TAU-1一般是稠密的；②當B關於求逆的性態很差時,直接約化會帶來很大誤差。對一次廣義特徵值問題已發展了不少其他有效解法而不必預先化到通常特徵值問題，一類是鬆弛法，包括逐次超鬆弛法、逐次坐標超鬆弛法和共軛梯度法等；另一類是變換方法,包括廣義雅可比方法、廣義吉文斯方法以及QZ方法等，後者是QR方法對一次廣義特徵值問題的直接推廣。
參考書目
　曹志浩著：《矩陣特徵值問題》，上海科學技術出版社，上海，1980。

配圖

相關連線