來源
“擬陣”這個詞是由Hassler Whitney最早開始使用的。他曾研究矩陣擬陣,其中S是給定矩陣的各個行,如果這些行在通常意義下是線性無關的,則他們是獨立的。
有限擬陣定義
有限擬陣有很多等價的定義方式。
獨立集
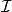 擬陣
擬陣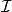 擬陣
擬陣Independent sets:就獨立來說, 一個有限的擬陣 M 是一個二元組 (E, ), 其中 E 是一個 有限集 (稱之為 基礎集) , 是一個由E的子集構成的集族 (稱之為獨立集) 它需要滿足下面的條件:
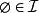 擬陣
擬陣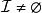 擬陣
擬陣1. 空集是獨立的, 也就是說, 。 換個說法就是, 至少有一個E的子集是獨立的, 即: 。
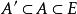 擬陣
擬陣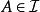 擬陣
擬陣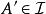 擬陣
擬陣2. 每個獨立集的子集是獨立的, 即: 對於每個子集 , 如果 則 . 有時我們稱之為遺傳特性。
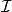 擬陣
擬陣3. 如果A和B是 的兩個獨立集,A比B有更多的元素, 則在A中存在一個元素,當其加入B時得到一個比B更大獨立集。有時我們稱之為擴充特性或者叫獨立集交換特性。
兩個特性定義了一個公認的組合結構,叫做獨立系統。
基與圈
Bases and circuits:E 對於一個基礎集的子集,如果它不是獨立的,那么我們稱它為不獨立集。對於擬陣M中的一個獨立集A,如果加入基礎集E中任何一個元素後,A都變為不獨立集,那么我們稱A是最大獨立集,也叫做擬陣的基。對於擬陣M中的一個不獨立集B,如果它的任何一個真子集都是獨立的,那么我們稱B是最小不獨立集,也叫做擬陣的圈。之所以這裡出現了圈,是因為擬陣中的圈正好與圖論中圖的環相對應。
 擬陣
擬陣 擬陣
擬陣 擬陣
擬陣獨立集,基或圈都能完整地描述擬陣:一個集合是獨立的若且唯若它不是不獨立集,若且唯若它是基的一個子集,若且唯若它不包含任何圈。不獨立集的集合,基的集合,圈的集合都擁有能作為擬陣公理的性質。例如,我們可以用元組(E, )定義擬陣M,其中E是一個有限集, 是E的子集的集合,我們稱之為“基集”, 有以下性質:
 擬陣
擬陣1. 不是空集。
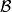 擬陣
擬陣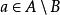 擬陣
擬陣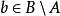 擬陣
擬陣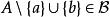 擬陣
擬陣2. 如果A和B是 中不同的元素,並且 ,那么存在一個元素 ,使得 (這裡的斜槓表示差集,該性質稱為基交換性質)。
 擬陣
擬陣根據基交換性質我們可以得出結論, 中沒有一個元素是其它元素的真子集。
秩函式
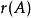 擬陣
擬陣Rank functions:兩個擬陣的基具有相同數量的元素,它是擬陣理論的一個基礎結論,這與線性代數中的基公理類似,基的元素的個數稱為似陣的秩。如果M是一個E上的擬陣,並且A是E的一個子集,那么A上的擬陣可以通過把一個A的子集當作是獨立集來定義若且唯若這個子集在M中是獨立集。這個性質使得我們可以討論子擬陣和E中任何子集的秩。子集A的秩通過秩函式 來定義,它有以下幾種性質:
1. 秩函式的值總是非負的。
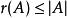 擬陣
擬陣2. 對於任意E的子集A,有 。
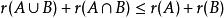 擬陣
擬陣3. 對於E的任意兩個子集A 和B ,有 。這意味著秩函式是一個子模函式。
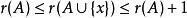 擬陣
擬陣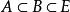 擬陣
擬陣4. 對於任意集合A和元素x,有 。從第一個不等式我們可以得到更一般的結論,如果 ,那么。這意味著秩函式是一個單調函式。
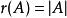 擬陣
擬陣這些屬性可以被用來替換有限擬陣的定義:如果(E,r)滿足這些屬性,那么E上的擬陣獨立集可以定義為E的子集A,且A滿足 。
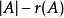 擬陣
擬陣子集A的元素個與其秩的差 叫作A的零化度(nullity)或補秩(corank)。它是從A中移除元素使得A成為獨立集的最小移除數量。E在擬陣M上的零化度叫做M的零化度或M的補秩。
閉包運算元
Closure operators:設M是有限集E上的一個擬陣,其秩函式有上述定義。E的子集A的閉包cl(A)的定義如下:
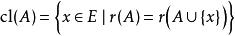 擬陣
擬陣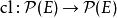 擬陣
擬陣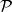 擬陣
擬陣閉包運算元 擁有如下性質,其中 表示冪集。
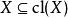 擬陣
擬陣1. 對於E的所有子集X,有 。
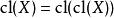 擬陣
擬陣2. 對於E的所有子集X,有 。
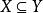 擬陣
擬陣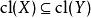 擬陣
擬陣3.對於E的所有子集X和Y,如果 ,那么 。
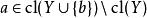 擬陣
擬陣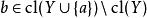 擬陣
擬陣4. 對於E的所有元素a和b,所有子集Y,如果 那么 。
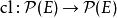 擬陣
擬陣前三個性質是閉包運算元的定義,第四個性質叫做Mac Lane–Steinitz交換性質。這些性質也可以當作是擬陣的另一個定義,每個遵守這些性質的 決定一個擬陣。
平面
Flats:我們稱閉包等於自身的集合是封閉的,這樣的集合也叫做擬陣的平面或子空間。如果一個集合的秩達到了最大,那么這個集合是封閉的,也就是說往該集合中加入任何元素都不會使它的秩變大。擬陣上的封閉的集合有以下性質:
1.E是封閉的。
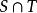 擬陣
擬陣2. 如果S和T都是平面,那么 也是一個平面。
3. 如果S是一個平面,那么平面T覆蓋S(意味著T真包含S但S和T間不存在平面U),劃分了E\S中的元素。
超平面
Hyperplanes:在一個秩為r的擬陣中,秩為r-1的平面稱為超平面,它是平面的最大真子集,也就是說超平面的唯一父集是E,它擁有擬陣的所有元素。超平面也叫做補原子(coatom),補原子是一個E的一個不能生成M子集,但往它加入任何元素都可以產生生成集。
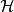 擬陣
擬陣擬陣的超平面系 擁有以下屬性,它也被認為是擬陣的另一個公理。
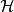 擬陣
擬陣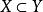 擬陣
擬陣1.超平面系 中不存在不同的使得 的X和Y,也就是說超平面是一個Sperner系。
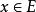 擬陣
擬陣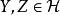 擬陣
擬陣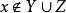 擬陣
擬陣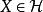 擬陣
擬陣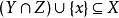 擬陣
擬陣2.對於每個 和不同的 ,如果 ,那么存在 ,並且有 。
樣例
均勻擬陣
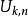 擬陣
擬陣Uniform matroids:設E是一個有限集,k是一個自然數。通過將E的每一個k-元素子集作為一個元素,我們可以定義一個關於E的擬陣。這被稱為秩為k的均勻擬陣。秩為k的,有n個元素的均勻擬陣記為 。秩大於等於2的所有均勻擬陣都是平凡的。n個點的秩為2的均勻擬陣被稱作n點線。一個擬陣是均勻的,若且唯若它沒有大小小於一加其秩的圈。均勻擬陣的直和稱為分區擬陣(partition matroids)。
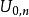 擬陣
擬陣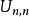 擬陣
擬陣在均勻擬陣 中,每一個元素都是一個循環(loop),在均勻擬陣 中,每一個元素都是一個聯合循環(coloop)。這兩種類型的擬陣的直和是一個分區擬陣,其中的每個元素都是循環或者聯合循環,被稱為離散擬陣(discrete matroids)。離散擬陣的一個等價定義是:E的每一個非空真子集都是一個分割。
擬陣與線性代數
擬陣理論主要來自於對向量空間中線性無關的維度的深層次屬性的考量。對於這種方式定義的擬陣,有兩種表示方法:
如果E是向量空間V的任意有限子集,通過將E中的線性無關子集作為M的元素,我們在E上定義擬陣M。這個擬陣的無關集合性質遵循斯坦尼茨交換定理。如果M是一個通過這種方式定義的擬陣,我們稱E表示M。這種類型的擬陣被稱作向量擬陣(vector matroids)。以這種方式定義的擬陣的一個重要的例子是法諾擬陣(Fano matroids),是由法諾平面(Fano Plane)衍生而來的秩為3的擬陣。它是一個其元素可以表示為有限域GF(2)上的三維向量空間中的七個非零的點的線性擬陣。然而,在GF(2) 上用無法用實數近似表達法諾擬陣。
由某個域中的元素組成的矩陣A,由其列組成的集合可以形成一個擬陣M。擬陣中線性相關的列的集合,即是作為向量線性相關的向量。這個擬陣被稱為A的列擬陣,也稱為A表示M。例如,法諾擬陣可以表示為一個3*7的0-1矩陣。列擬陣是向量擬陣的另一種叫法,然而在進行矩陣表示時,這種表達方式更常用。
一個等價於向量擬陣的擬陣,儘管其表示可能不同,被稱為可表示的或者線性的。如果在域F上,擬陣M等價於一個向量擬陣,我們稱F上M是可表示的。特別地,M是可實數表示的如果它在實數域上是可表示的。例如,儘管一個圖擬陣是以圖的角度表示的,它也可以通過其他域上的向量來表示。擬陣理論的一個基本問題是在給定的域F刻畫其可表示的擬陣的特徵。Rota推論給出了有限域上的可能的刻畫,迄今的主要成果是二項擬陣的特徵。
一個常規擬陣(regular matroid)是在所有域上都可表示的擬陣。Vámos擬陣是在任何域上都不可表示的擬陣的一個簡單例子。
擬陣與圖理論
擬陣理論的另一個來源是圖理論。
每一個有限圖G都以以下方式給出一個擬陣M(G):將圖G中的所有邊作為集合E,若且唯若一個邊構成的集合是森林時,認為其是獨立的;也就是說,若且唯若其不包含簡單環路。那么M(G)被稱作一個環擬陣。以這種方式構造的擬陣為圖擬陣(graphic matroids)。並非每個擬陣都是圖擬陣,但是所有三個元素組成的擬陣都是圖擬陣。每個圖擬陣都是常規擬陣。
後來人們在圖結構中發現了很多擬陣:雙環擬陣由獨立性定義為至多包含一個環的連通子集構成。
在任何有向圖或無向圖G中,記E和F是兩個不重合的頂點集。在集合E中,定義子集U是獨立的,如果從F到U有|U|條頂點不相交路徑。這種E上定義的擬陣稱為gammoid:一個嚴格的gammoid是E為G的全部頂點的集合。
在一個二分圖G=(U, V, E)中,我們可以定義擬陣:元素為U中的頂點,獨立子集為圖中頂點匹配的集合。這種擬陣被稱為transversal matroid,是gammoid的一個特例。
拉曼圖形成了二維的堅固擬陣,這種擬陣是結構穩定的。
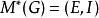 擬陣
擬陣設G是一個連通圖,E是它的邊集。記I是E的滿足以下條件的子集F的集合:G-F是連通圖。那么 是一個擬陣,稱為G的bond matroid。注意秩函式r(F)是邊集F產生的子圖中的最小環的個數。
擬陣與域擴張
擬陣理論的第三個來源是域理論。
域的一個擴張可以給出一個擬陣。假設F和K是K包含F的兩個域。設E是K的任意有限子集。定義E的子集S是代數獨立的如果域擴張F(S)的超越次數等於|S|。
與這種定義下的擬陣等價的擬陣被稱作代數擬陣(algebraic matroid)。刻畫代數擬陣的問題非常困難,相關知識很少。Vámos擬陣是一個非代數擬陣的例子。
基本構造
有很多種標準的方式能夠從已有的擬陣中構造新的擬陣。
對偶
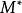 擬陣
擬陣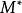 擬陣
擬陣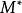 擬陣
擬陣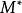 擬陣
擬陣Duality:如果M是一個有限擬陣,我們可以定義其正交擬陣或者對偶擬陣 ,通過使用相同的原始集合,而一個集合在 中若且唯若其補集在M中。不難驗證 是一個擬陣,而且 的對偶擬陣是M。
對偶擬陣也可以通過其他定義擬陣的方式來很好的描述,比如:
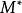 擬陣
擬陣中的一個集合是獨立的,若且唯若它的補集在M中是非獨立的
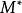 擬陣
擬陣中的一個集合是環,若且唯若他的補集在M中是聯合原子性的
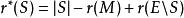 擬陣
擬陣對偶矩陣的秩函式是
 擬陣
擬陣根據庫拉托夫斯基定理的擬陣版本,圖擬陣 的對偶擬陣也是圖擬陣,若且唯若M是平面圖的圖擬陣。這種情況下,M的對偶擬陣是G的對偶圖的擬陣。特定域F上可表示的向量擬陣的對偶擬陣在F上也是可表示的。中的頂點,獨立子集為圖中頂點匹配的集合。這種擬陣被稱為transversal擬陣的對偶擬陣也是嚴格的gammoid,反之亦然。
極小元
Minors:如果M是基於集合E 的擬陣,S是E的一個子集,將M限定到S,記做M|S,是S上的擬陣,其獨立集合是S中所包含的M的獨立集合。它的環是S中所包含的M的環。他的秩函式是M限定到S的秩函式。線上性代數中,這對應著將向量空間限定到由S中的向量組成的空間。等價地,如果T=M-S,這表示刪除T,寫做M\T或者M-T。M的子擬陣是一系列減法的結果,而且順序是無關的。
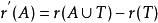 擬陣
擬陣限定的對偶操作是縮減。如果T是E的子集,M的T縮減,記做M/T,是原始集合E-T的擬陣,其秩函式是 。線上性代數中,這對應著由T中的向量與E-T的向量的像形成的商空間。
 擬陣
擬陣由 經過一些列的限制和縮減操作得到的擬陣N稱為M的一個極小元。我們稱M包含一個極小元N。很多重要的擬陣系都可以用不屬於此系的極小元-最小值擬陣來刻畫,這些擬陣稱為禁止擬陣或排除擬陣。
和與並
Sums and unions:設M是原始集合為E的擬陣,設N是原始集合為F的擬陣。M和N的直和是原始集合為E和F的不相交並集的擬陣,其獨立集合是M和N的獨立集合的不相交並集。
M和N的並,是原始集合為E和F的並集的擬陣,它的獨立集合是M和N的獨立集合的並集。通常“並”在E=F時使用,但這個假設不是必要的。如果E和F是不相交的,M和N的並即是其直和。
相關術語
設M是由元素集合E構成的擬陣。
E可能被稱作M的基礎集。它的元素可能被稱作M的點。
一個E的子集涵蓋了M,如果M的閉包是F。一個集合被叫做涵蓋了一個封閉集合K,當它的閉包是K,擬陣的周長(girth)是它最小的圈或者獨立子集的大小。
一個組成了M的單個元素圈的元素稱之為環。同等的,一個元素是一個環,當它不屬於任何基(basis)。
一個不屬於任何圈的元素被成為一個聯合環或者峽(isthmus)。同等的,一個元素是個聯合環,當它屬於每一個基(basis)。環和聯合環是互相對偶。
如果兩個元素集合{f,g}是M的一個圈,那么f和g在M中是平行的。
一個擬陣被稱作是簡單的,當它沒有包含1或2個元素的圈。也就是說,這個擬陣沒有任何環或者沒有平行元素。這個意義也被組合集合學使用。一個簡單擬陣的獲得方法是從另外一個擬陣M中刪除所有的環和從每個二元圈中刪除一個元素直到沒有留下二元圈為止,這個過程被成為M的簡化。一個擬陣是聯合簡單的,當它的對偶擬陣也是簡單的。
一個圈的並操作有時候也被稱作M的環。一個環因此是一個對偶擬陣的平面(flat)的補(此處的使用跟在圖理論中通常的圈定義是衝突的)。
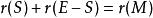 擬陣
擬陣一個M的分隔設定是S的一個子集,滿足 。一個真或者非平凡的分隔設定是既不是M又不是空集的分隔設定。一個不可歸約的分隔設定是沒有包含任何非空的分隔設定的分隔設定。不可歸約的分隔設定劃分了基礎集E。
一個不能被直接寫成兩個非空擬陣直接相加結果的擬陣,或者同等的,沒有真分隔設定,被稱為相連,或者不可歸約。一個擬陣被相連的,若且唯若它的對偶是相連的。
一個最大的不可歸約的M的子擬陣被稱為M的分量。一個分量是從M到一個不可歸約的分隔設定的約束,相反的,從M到一個不可歸約的分隔設定的約束是一個分量。一個分隔設定就是所有分量的是並。
一個擬陣M被稱作幀擬陣,當它或者一個包含有它的擬陣,有一個基(basis)因此所有的M的點在基(basis)元素對的交點的線上被包含。
一個擬陣被稱為平鋪矩陣,當它的所有圈有著至少等於它的秩的大小。
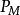 擬陣
擬陣一個擬陣多胞形 是基於M的指標向量的凸包。
套用
擬陣可以用來研究貪心算法,他是貪心算法的數學基礎,可以這么說,一個問題如果他可以轉換為擬陣,那么一定可以用貪心算法進行求解;但是並不是所有的可用貪心算法求解的問題都能轉換為擬陣。
主要是用來求解最優問題,是組合最佳化問題的有力工具。
算法
貪心算法
一個帶權擬陣是一種帶有映射函式,將其元素映射到非負實數上的擬陣。一個元素的子集的權重被定義為在子集上的所有元素權重之和。貪心算法可以被用於找到一個擬陣的最大權重基,通過從空集開始,疊代地一次添加一個元素,在每一步中從所有能夠保持增廣集獨立性的元素中選擇一個最大權重的元素。這個算法不需要知道任何有關擬陣定義的細節,只要通過獨立定義,即測試一個集合是否是獨立的子例程來跟擬陣打交道。
一個最佳化算法可能被用來表示擬陣的特點:如果一個集合的簇F,在取子集的情況下,具有這樣的性質,不管集合權重是多少,貪心算法從簇中找到最大權重的集合,那么F一定是一個擬陣的獨立子集的簇。
擬陣的概念已經被推廣在允許其他類型的集合上,通過貪心算法獲得最佳化解決方案。
擬陣劃分
擬陣劃分問題是指,把一個擬陣當中的元素劃分到儘可能少的獨立子集當中,擬陣打包問題是找到儘可能多的不相交生成集。這兩者都可以在多項式時間內解決,可以被推廣到計算秩或者找到擬陣和中的一個最大獨立子集問題中。
擬陣相交
兩個或者更多的擬陣相交是在每個擬陣中的集合系都同時獨立。找到在兩個擬陣的交中最大集,或者最大帶權集的問題是在多項式時間可得到結果,並提供了一個解決許多其他重要的組合最佳化問題的方法。比如,在二分圖中的最大匹配問題可以被表述為兩個劃分擬陣的交的問題。然而,在三個或者更多擬陣的交中找到最大集的問題是NP完全的。
擬陣軟體
兩個用於做擬陣運算的單機系統是Kingan的Oid和Hlineny的Macek。他們兩者都是開源包。Oid是一個互動式的,可擴展的軟體系統,被用於擬陣實驗。Macek是一個由許多工具和例程構成的軟體系統,在可表示的擬陣上可以高效地進行組合計算。
SAGE是一個開源的數學軟體系統,包括了擬陣的包。
無限擬陣
無限擬陣遠遠比有限擬陣複雜,在很長一段時間內,業界存在很多合理的有用的定義,但沒有一個能概括有限擬陣的所有重要性質的理論。例如,在無限擬陣中,似乎沒有基,圈和對偶等概念。
無限擬陣最簡單的定義是需要有限的秩,也就是說E的秩是有限的。除了對偶性之外,這個理論與有限擬陣相似,因為有限秩的無限擬陣的對偶不存在有限的秩。有限秩的擬陣包括有限維度向量空間,域擴張和有限超越次數的每個子集。
一個具有限性質的擬陣有如下性質:
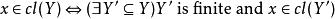 擬陣
擬陣也就是說,每個非獨立集包括一個有限的非獨立集。
無限擬陣的獨立性質有以下幾個公理:
1. 空集是獨立的。
2. 每個獨立集的子集是獨立的。
 擬陣
擬陣 擬陣
擬陣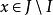 擬陣
擬陣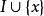 擬陣
擬陣3. 對於每個非最大獨立集 和最大獨立集 , 如果 ,那么 是獨立的。
 擬陣
擬陣 擬陣
擬陣 擬陣
擬陣 擬陣
擬陣4. 對於基空間的每個子集 ,每個 的獨立子集 可以擴展成 的最大獨立子集。
在這些公理存在的前提下,每個擬陣都有一個對偶。
相關研究
(1)模糊擬陣中若干問題的研究
(2)擬陣與圖
(3)擬陣約束下的劃分問題的研究

