基本介紹
因子旋轉(factor rotation)是一種變換,就是旋轉因子的坐標軸。在因子分析中,當求得公共因子及其因子載荷陣後,對公因子要給出具有實際意義的合理解釋。如果公共因子難以和實際問題相對應,可對公因子進行旋轉,使得旋轉後的公因子具有實際意義。常用的旋轉方法有兩種:方差極大的正交旋轉;方差極大的斜交旋轉 。
詳細說明
旋轉的目的與方法
建立因子分析模型的目的不僅是找出主因子,更重要的是知道每個主因子的意義,以便對實際問題進行分析。如果求出主因子後,各個主因子的典型代表變數不是很突出,還需要進行因子旋轉,通過適當的旋轉得到比較滿意的主因子 。
因子旋轉的方法有很多, 正交旋 轉(orthogonal rotation)和 斜交旋 轉(oblique rotation)是因子旋轉的兩類方法。最常用的方法是最大方差正交旋轉(Varimax)法。進行因子旋轉,就是要使因子載荷矩陣中因子載荷的絕對值向0和1兩個方向分化,使大的載倚更大,小的載荷更小。因子旋轉過程中,如果因子對應軸相互正交,則稱為正交旋轉;如果因子對應軸相互間不是正交的,則稱為斜交旋轉。常見的斜交旋轉方法有Promax法等。
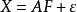 因子旋轉
因子旋轉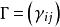 因子旋轉
因子旋轉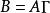 因子旋轉
因子旋轉若已經求得因子分析模型為,設為一正交矩陣,作正交變換,可以證明,
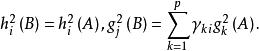 因子旋轉
因子旋轉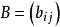 因子旋轉
因子旋轉其中。
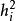 因子旋轉
因子旋轉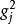 因子旋轉
因子旋轉這表明經過正交旋轉後,共同度並不改變,但公共因子的方差貢獻不再與原來相同。這樣我們就可以對因子進行合理的解釋了。
 因子旋轉
因子旋轉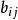 因子旋轉
因子旋轉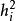 因子旋轉
因子旋轉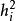 因子旋轉
因子旋轉 因子旋轉
因子旋轉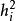 因子旋轉
因子旋轉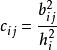 因子旋轉
因子旋轉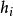 因子旋轉
因子旋轉 因子旋轉
因子旋轉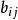 因子旋轉
因子旋轉對已知的因子載荷矩陣進行正交變換的目的是使各因子上的載荷兩極分化,也就是要使各個因子上的載荷之間方差極大化。由於各個變數在某因子上的載荷的平方是該因子對該變數的共性方差的貢獻,而各變數的共性方差一般又互不相同,若某個變數的共性方差較大,則分配在各個因子上的載荷就大些;反之,則小些。因此,為了消除各個變數的共性方差大小的影響,計算某因子上的載荷的方差時,可先將各個載荷的平方除以共性方差,即類似於將其標準化,然後再計算標準化後的載荷的’方差,記為。選擇除以是為了消除各個原始變數對公共因子依賴程度不同的影響,而且這樣的選擇還不影響因子的共同度。取平方的目的是消除符號不同的影響。
對於某一因子j,可定義其載荷之間的方差為:
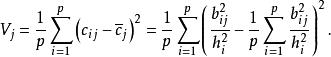 因子旋轉
因子旋轉全部公共因子各自載荷之間的總方差為:
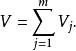 因子旋轉
因子旋轉 因子旋轉
因子旋轉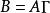 因子旋轉
因子旋轉現在就是要尋找一個正交矩陣,經過對已知的載荷矩陣A的正交變換後,新的因子載簡矩陣中的元素能使V取得極大值 。
方差極大的正交旋轉
記因子載荷陣為
 因子旋轉
因子旋轉變數x的公因子方差為
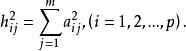 因子旋轉
因子旋轉稱
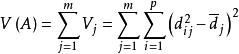 因子旋轉
因子旋轉為因子載荷陣A的總方差,其中
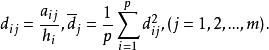 因子旋轉
因子旋轉 因子旋轉
因子旋轉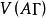 因子旋轉
因子旋轉當每個因子的載荷(即A中每一列)的絕對值趨於0或1時,V(A)值就大,這時相應的公共因子具有簡單的結構。所謂方差極大的正交旋轉,即選擇正交陣,使達最大。當m=2時,正交陣可表為
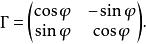 因子旋轉
因子旋轉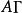 因子旋轉
因子旋轉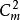 因子旋轉
因子旋轉適當地選擇旋轉角度φ,可使的總方差達最大;當m>2時,可逐次對每兩個因子進行旋轉,m個公因子全部配對旋轉,共需旋轉次。全部旋轉完結稱為一輪(或一個循環,一圈),一輪完成後再繼續做下一輪,每輪後,總方差單調不減且有界,因此,該算法一定收斂,在實際計算時,當V值變化不大時,可停止旋轉 。
方差極大的斜交旋轉
若正交旋轉後的公因子仍然沒有明顯的實際意義,亦可作方差極大的斜交旋轉,選擇適當的非退化矩陣P(P非正交陣),使AP的總方差達最大的變換稱為方差極大的斜交旋轉,變換矩陣P是一般的非奇異矩陣,故具有更大的選擇性。具體旋轉方法與方差極大的正交旋轉相同 。

