多項式
在數學中,多項式(polynomial)是指由變數、係數以及它們之間的加、減、乘、冪運算(正整數次方)得到的表達式。
對於比較廣義的定義,1個或0個單項式的和也算多項式。按這個定義,多項式就是整式。實際上,還沒有一個只對狹義多項式起作用,對單項式不起作用的定理。0作為多項式時,次數定義為負無窮大(或0)。單項式和多項式統稱為整式。
多項式中不含字母的項叫做常數項。如:5X+6中的6就是常數項。
幾何特性
多項式是簡單的連續函式,它是平滑的,它的微分也必定是多項式。泰勒多項式的精神便在於以多項式逼近一個平滑函式,此外閉區間上的連續函式都可以寫成多項式的均勻極限。
定理
基本定理
代數基本定理是指所有一元n次(複數)多項式都有n個(複數)根。高斯引理
兩個本原多項式的乘積是本原多項式。套用高斯引理可證,如果一個整係數多項式可以分解為兩個次數較低的有理係數多項式的乘積,那么它一定可以分解為兩個整係數多項式的乘積。這個結論可用來判斷有理係數多項式的不可約性。關於Q[x]中多項式的不可約性的判斷,還有艾森斯坦判別法:對於整係數多項式,如果有一個素數p能整除αn-1,αn-2,…,α1,α0,但不能整除αn,且pˆ2不能整除常數項α0,那么ƒ(x)在Q上是不可約的。由此可知,對於任一自然數n,在有理數域上xn-2是不可約的。因而,對任一自然數n,都有n次不可約的有理係數多項式。
分解定理
F[x]中任一個次數不小於1的多項式都可以分解為F上的不可約多項式的乘積,而且除去因式的次序以及常數因子外,分解的方法是惟一的。當F是複數域C時,根據代數基本定理,可證C[x]中不可約多項式都是一次的。因此,每個復係數多項式都可分解成一次因式的連乘積。
當F是實數域R時,由於實係數多項式的虛根是成對出現的,即虛根的共軛數仍是根,因此R[x]中不可約多項式是一次的或二次的。所以每個實係數多項式都可以分解成一些一次和二次的不可約多項式的乘積。實係數二次多項式αx2+bx+с不可約的充分必要條件是其判別式b2-4αс<0。
當F是有理數域Q時,情況複雜得多。要判斷一個有理係數多項式是否不可約,就較困難。套用本原多項式理論,可把有理係數多項式的分解問題化為整係數多項式的分解問題。一個整係數多項式如其係數是互素的,則稱之為本原多項式。每個有理係數多項式都可表成一個有理數及一個本原多項式的乘積。關於本原多項式有下述重要性質。
正文
代數學中最基本的研究對象之一。設αi(i=0,1,…,n)是域F中元素,x是一個文字(或稱符號),則形如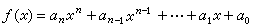 的表示式,稱為F上的一個文字x的多項式,簡稱為一元多項式。αn,αn-1,…,α1,α0稱為ƒ(x)的係數,αkxk 稱為k次項,αk稱為k次項係數。如果αn≠0,那么ƒ(x)稱為n次多項式,此時αnxn 稱為ƒ(x)的首項,αn稱為ƒ(x)的首項係數。兩個多項式相等是指它們的同次項的係數都相等。係數全為零的多項式,稱為零多項式,記作0,並約定零多項式的次數為-
的表示式,稱為F上的一個文字x的多項式,簡稱為一元多項式。αn,αn-1,…,α1,α0稱為ƒ(x)的係數,αkxk 稱為k次項,αk稱為k次項係數。如果αn≠0,那么ƒ(x)稱為n次多項式,此時αnxn 稱為ƒ(x)的首項,αn稱為ƒ(x)的首項係數。兩個多項式相等是指它們的同次項的係數都相等。係數全為零的多項式,稱為零多項式,記作0,並約定零多項式的次數為- 。
。 F上的兩個多項式
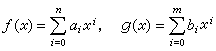
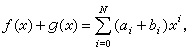 (1)
(1)
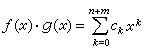 (2)
(2)
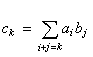 。
。 用F【x】表示係數在域F中的多項式全體,用公式(1)、(2)定義F【x】的加法以及乘法,則F【x】成一個環,稱之為F上的一元多項式環。F【x】是具有單位元素的整環。
設ƒ(x)和g(x)是F【x】中的兩個多項式,若存在F【x】中一個多項式q(x),使得ƒ(x)=q(x)g(x),則稱ƒ(x)是g(x)的一個倍式,g(x)是ƒ(x)的一個因式。套用帶餘除法可以判斷g(x)是否是ƒ(x)的一個因式。
帶餘除法 若 ƒ(x)和g(x)是F【x】中的兩個多項式,且 g(x)≠0,則在F【x】中有多項式 q(x)和r(x),滿足ƒ(x)=q(x)g(x)+r(x),其中r(x)的次數小於g(x)的次數,且只有一對q(x)和r(x)滿足這些條件。此時q(x) 稱為g(x)除ƒ(x)的商式,r(x)稱為餘式。當g(x)=x-α時,則r(x)=ƒ(α)稱為余元,式中的α是F的元素。此時帶餘除法具有形式ƒ(x)=q(x)(x-α)+ƒ(α),稱為余元定理。g(x)是ƒ(x)的因式的充分必要條件是g(x)除ƒ(x)所得餘式等於零。如果g(x)是ƒ(x)的因式,那么也稱g(x) 能整除ƒ(x),或ƒ(x)能被g(x)整除。特別地,x-α是ƒ(x)的因式的充分必要條件是ƒ(α)=0,這時稱α是ƒ(x)的一個根。
如果d(x)既是ƒ(x)的因式,又是g(x)的因式,那么稱d(x)是ƒ(x)與g(x)的一個公因式。如果d(x)是ƒ(x)與g(x)的一個公因式,並且ƒ(x)與g(x)的任一個因式都是d(x)的因式,那么稱d(x)是ƒ(x)與g(x)的一個最大公因式。如果ƒ(x)=0,那么g(x)就是ƒ(x)與g(x)的一個最大公因式。當ƒ(x)與g(x)全不為零時,可以套用輾轉相除法來求它們的最大公因式。
輾轉相除法 已知 F【x】 中兩個不等於零的多項式ƒ(x)與g(x),用g(x)除ƒ(x)得商式q1(x)、餘式r1(x)。若r1(x)=0,則g(x)就是ƒ(x)與g(x)的一個最大公因式。若 r1(x)≠0,則用 r1(x)除 g(x)得商式q2(x)、餘式r2(x)。若r2(x)=0,則r1就是ƒ(x)與g(x)的一個最大公因式。否則,如此輾轉相除下去,餘式的次數不斷降低,經有限s次之後,必有餘式為零,即有如下的一組等式:

利用輾轉相除法的算法,可將ƒ(x)與g(x)的最大公因式rs(x)表成ƒ(x)和g(x)的組合,而組合的係數是F上的多項式。
如果ƒ(x)與g(x)的最大公因式是零次多項式,那么稱ƒ(x)與g(x)是互素的。最大公因式和互素概念都可以推廣到幾個多項式的情形。
如果F【x】中的一個次數不小於1的多項式ƒ(x),不能表成 F【x】 中的兩個次數較低的多項式的乘積,那么稱ƒ(x)是F上的一個不可約多項式。
任一多項式都可分解為不可約多項式的乘積。
惟一分解定理 F【x】中任一個次數不小於 1的多項式都可以分解為F上的不可約多項式的乘積,而且除去因式的次序以及常數因子外,分解的方法是惟一的。
當F是複數域C時,根據代數基本定理,可證C【x】中不可約多項式都是一次的。因此,每個復係數多項式都可分解成一次因式的連乘積。
當F是實數域R時,由於實係數多項式的虛根是成對出現的,即虛根的共軛數仍是根,因此R【x】中不可約多項式是一次的或二次的。所以每個實係數多項式都可以分解成一些一次和二次的不可約多項式的乘積。實係數二次多項式αx2 +bx+с不可約的充分必要條件是其判別式b2 -4αс<0。
當F是有理數域Q時,情況複雜得多。要判斷一個有理係數多項式是否不可約,就較困難。套用本原多項式理論,可把有理係數多項式的分解問題化為整係數多項式的分解問題。一個整係數多項式如其係數是互素的,則稱之為本原多項式。每個有理係數多項式都可表成一個有理數及一個本原多項式的乘積。關於本原多項式有下述重要性質。
高斯引理:兩個本原多項式的乘積是本原多項式。
套用高斯引理可證,如果一個整係數多項式可以分解為兩個次數較低的有理係數多項式的乘積,那么它一定可以分解為兩個整係數多項式的乘積。這個結論可用來判斷有理係數多項式的不可約性。關於Q【x】中多項式的不可約性的判斷,還有艾森斯坦判別法:對於整係數多項式
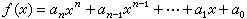 ,如果有一個素數p能整除αn-1,αn-2,…,α1,α0,但不能整除αn,且p2 不能整除常數項α0,那么ƒ(x)在Q上是不可約的。由此可知,對於任一自然數n,在有理數域上xn -2是不可約的。因而,對任一自然數n,都有n次不可約的有理係數多項式。
,如果有一個素數p能整除αn-1,αn-2,…,α1,α0,但不能整除αn,且p2 不能整除常數項α0,那么ƒ(x)在Q上是不可約的。由此可知,對於任一自然數n,在有理數域上xn -2是不可約的。因而,對任一自然數n,都有n次不可約的有理係數多項式。 多項式方程 多項式理論的發展與多項式方程(代數方程)的研究有密切聯繫。一個未知量的高次方程的一般形式為
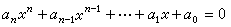 (3)
(3)
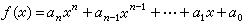 於是方程(3)的根即多項式ƒ(x)的根。
於是方程(3)的根即多項式ƒ(x)的根。 在20世紀以前,解方程一直是代數學的一個中心問題。遠在公元以前,文明古國的學者對於某些特殊二次方程的解法,已經有所研究。在16世紀才得到三次方程和四次方程的解法。
二次方程αx2 +bx+с=0的求根公式為
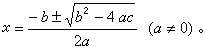 (4)
(4)
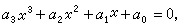 (5)
(5)
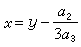 將(5)化為
將(5)化為  (6)
(6)
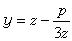 ,將(6)化為關於 z3 的二次方程
,將(6)化為關於 z3 的二次方程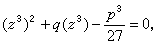 套用公式(4)求出z3 ,即可得出方程(6)的三個根為
套用公式(4)求出z3 ,即可得出方程(6)的三個根為 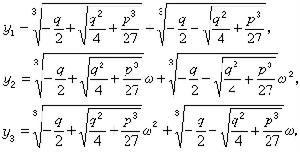
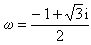 。因此方程(5)的根為
。因此方程(5)的根為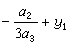 ,
,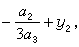
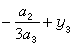 。求解四次方程
。求解四次方程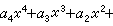
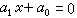 ,把它的根減去
,把它的根減去 而化為
而化為 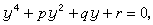 (7)
(7)
 比較兩端各項的係數,得
比較兩端各項的係數,得 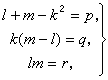 (8)
(8)
 (9)
(9)
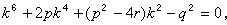
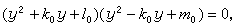
 就得出原方程的四個根。
就得出原方程的四個根。 一個代數方程的解,如果可以由這個方程的係數經過有限次加減乘除以及開整數次方等運算表示出來,就稱為這個方程的根式解。一、二、三、四次代數方程都有根式解,而五次和五次以上的代數方程就沒有根式解(見伽羅瓦理論)。
根據多項式的根與一次因式的關係以及關於復係數和實係數多項式的因式分解定理,有以下結論:
每個復係數n次方程恰有n個復根(重根按重數計算)。
如果虛數α是實係數方程ƒ(x)=0的一個根,那么ā(α的共軛數)也是這個方程的根,並且它們的重數也是相同的。
有理係數高次方程的求解,可歸結為整係數方程的求解問題。如果有理數r/s是整係數方程(3)的一個有理根,其中r和s是互素的整數,那么r一定是α0的因數, s一定是αn的因數。特別地,若ƒ(x)的首項係數為1,則它的有理根都是整根,而且是常數項的因數。
插值多項式 在實際問題中,往往通過實驗或觀測得出表示某種規律的數量關係y=F(x),通常只給出了F(x)在某些點xi上的函式值yi=F(xi),j=1,2,…,n+1。即使有時給出了函式F(x)的解析表達式,倘若較為複雜,也不便於計算。因此,需要根據給定點 xi 上的函式值F(xi),求出一個既能反映F(x)的特性,又便於計算的簡單函式ƒ(x)來近似地代替F(x),此時ƒ(x)稱為F(x)的插值函式;x1,x2,…,xn+1,稱為插值節點。求插值函式的方法,稱為插值法。
多項式是一類簡單的初等函式,而且任給兩組數:b1,b2,…,bn+1和各不相同的 с1,с2,…,сn+1,總有惟一的次數不超過n的多項式ƒ(x)滿足ƒ(сi)=bi,i=1,2,…,n+1。因此在實際套用中常常取多項式作為插值函式。作為插值函式的多項式,稱為插值多項式。插值多項式在計算數學插值中最常用。
多元多項式 設α是域F中元素,x1,x2,…,xn是無關的文字。形如
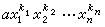 (10)
(10)
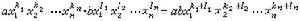 。
。 有限個單項式之和稱為多元多項式,簡稱多項式。不同類的單項式之和表示的多項式,其中係數不為零的單項式的最高次數,稱為此多項式的次數。
多項式的加法,是指多項式的同類項的係數相加(即合併同類項)。多項式的乘法,是指把一個多項式中的每個單項式與另一個多項式中的每個單項式相乘之後相加,且合併同類項。
F上x1,x2,…,xn的多項式全體所成的集合F【x1,x2,…,xn】,對於多項式的加法和乘法成為一個環,是具有單位元素的整環。
域上的多元多項式也有因式分解惟一性定理。
對稱多項式 它在多元多項式中占有重要地位。如果多元多項式ƒ(x1,x2,…,xn)對於1,2,…,n的任一個排列i1,i2,…,in,都有
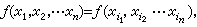 那么ƒ(x1,x2,…,xn)稱為對稱多項式。一元多項式根的研究,是對稱多項式的來源之一,也是它套用的一個重要方面。以下的n元多項式稱為初等對稱多項式:
那么ƒ(x1,x2,…,xn)稱為對稱多項式。一元多項式根的研究,是對稱多項式的來源之一,也是它套用的一個重要方面。以下的n元多項式稱為初等對稱多項式: 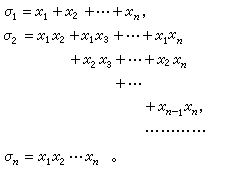
F【x1,x2,…,xn】中所有對稱多項式組成F【x1,x2,…,xn】的一個子環。
一元多項式和多元多項式都可以推廣到係數屬於某個環的情形。特別,係數在數域中的多項式環,是各種環的一類很重要的例子。

