定義
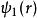 正交性
正交性 正交性
正交性 正交性
正交性如果兩個函式和滿足條件:,則稱這兩個函式相互正交。
量子力學表明:屬於同一厄米算符的不同本徵值的本徵函式互相正交。這種性質稱為本徵函式的 正交性。
“正交性”是從幾何中借來的術語。如果兩條直線相交成直角,他們就是正交的。用向量術語來說,這兩條直線互不依賴。沿著某一條直線移動,該直線投影到另一條直線上的位置不變。
在計算技術中,該術語用於表示某種不相依賴性或者解耦性。如果兩個或者更多事物中的一個發生變化,不會影響其他事物。這些事物就是正交的。在設計良好的系統中,資料庫代碼與用戶界面是正交的:你可以改變界面,而不影響資料庫,或者更換資料庫,而不用改變界面。
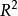 正交性
正交性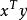 正交性
正交性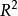 正交性
正交性 正交性
正交性 正交性
正交性我們可以通過定義一個標量積或內積在向量空間上增加結構的概念。因為對每一對向量,這種乘積得到一個標量,而不是第三個向量,因此,它並不是真正的向量乘法。例如,在 (二維向量空間)中,可以定義兩個向量x和y的標量積為 。可以認為 中的向量為從原點出發的有向線段。不難證明,兩個線段的夾角為直角的充要條件是兩個向量對應的標量積為零。一般地,若 為定義了標量積的向量空間,且 中的兩個向量的標量積為零,則稱它們正交(orthogonal)。
 正交
正交 正交性
正交性 正交性
正交性 正交性
正交性 正交性
正交性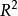 正交性
正交性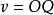 正交性
正交性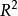 正交性
正交性 正交性
正交性 正交性
正交性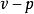 正交性
正交性 正交性
正交性 正交性
正交性 正交性
正交性 正交性
正交性 正交性
正交性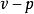 正交性
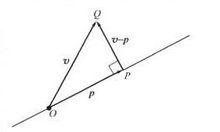
正交性可以將正交性理解為任何定義了內積的向量空間中垂直(perpendicularity)概念的推廣。為看到這樣做的重要意義,考慮如下的問題。令 為一通過原點的直線,並令Q不是 上的點。求 上離Q點最近的點P。這個問題中所求的點P的特徵是,QP垂直於OP(見圖5.0.1)。如果將直線 看成 的一個子空間,且 為 中的向量,則問題化為在子空間中求一向量使得它最“接近” 。解P的特徵將是 與 正交(見圖5.0.1)。通過在向量空間中引入內積,我們可以考慮一般的最小二乘(leastsquare)問題。在這些問題中,給定了一個 中的向量和一個子空間 。我們希望在 中尋找與v最“接近”的向量。解必 與 正交。這個正交性條件提供了求解最小二乘問題的關鍵最小二乘問題常常出現在很多涉及數據擬合的統計套用中。
相關概念
 正交性的相關概念
正交性的相關概念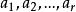 正交性
正交性1.正交向量組:設n維向量是一組兩兩正交的非零向量組,則稱這個向量組為正交向量組。若其中每一個向量都是單位向量,則稱向量組為標準正交向量組或規範正交向量組。
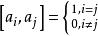 正交性
正交性因此,一個向量組是規範正交向量組的充要條件是.
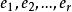 正交性
正交性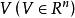 正交性
正交性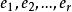 正交性
正交性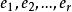 正交性
正交性 正交性
正交性2.標準正交基:設n維向量是向量空間的一個基,若兩兩正交,且均為單位向量,則稱為的一個標準正交基(或規範正交基)。
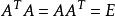 正交性
正交性3.正交矩陣:若n階方陣A滿足,則稱A為正交矩陣,簡稱正交陣。
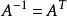 正交性
正交性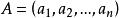 正交性
正交性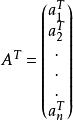 正交性
正交性由以上定義易知正交陣A可逆,且,此外i,若,則,
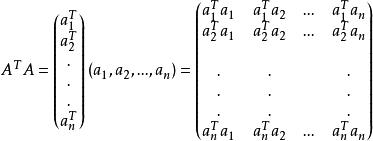 正交性
正交性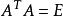 正交性
正交性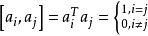 正交性
正交性由,故.
 正交性
正交性即正交陣A的列向量組為規範正交向量組。
正交化方法
 正交性
正交性 正交性
正交性將向量空間的任一基(線性無關)轉換為一正交規範基的方法如下:
 正交性
正交性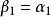 正交性
正交性(1)首先利用施密特正交化方法將正交化,即取,
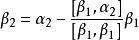 正交性
正交性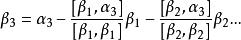 正交性
正交性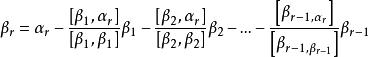 正交性
正交性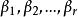 正交性
正交性則為正交基。
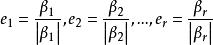 正交性
正交性(2)然後將它們單位化,即令
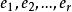 正交性
正交性 正交性
正交性則即為的正交規範基。
