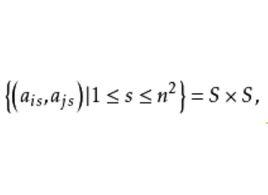基本介紹
定義1 設n≥1,k≥2,A為n元集S上的一個k×n 矩陣:
 正交陣列
正交陣列若對任意1≤i<j≤k,A的第i行與第j行都正交,即
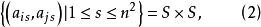 正交陣列
正交陣列則稱A是集合S上一個約束數(constraint)為k的n階 正交陣列(orthogonal array)。記作OA(n,1;k)。
正交陣列與正交拉丁方的關係
關於正交陣列與正交拉丁方之間的關係。我們有下述引理 :
引理1 OA(n,1;k)的存在性等價於(k-2)-MOLS(n)的存在性。
證 若(k-2)-MOLS(n)存在,不失一般性,可設A,A,…,A為集合S=Z上k-2個兩兩正交的n階拉丁方:
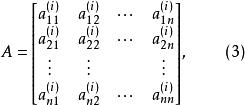 正交陣列
正交陣列其中1≤i≤k-2,設s=k-2,在集合S上構作如下k×n 陣列A:
 正交陣列
正交陣列由引理1及A,A,…,A的正交性可知A是S上的一個OA(n,1;k)。
反之。設A是S上的一個OA(n,1;k),由於交換A中任意兩列後仍得到一個OA(n,1;k)。故不妨設A的前兩行即為式(4)中陣列的前兩行。由它們分別給出R與C,然後對1≤i≤k-2。由A的第i+2行相應作出n×n矩陣A.由OA(n,1;k)中各行的正交性可知A,A,…,A即為一組(k-2)-MOLS(n)。
正交陣列與橫截設計的關係
下面討論正交陣列與橫截設計之間的關係 。
引理2 存在OA(n,1;k)的充分必要條件為存在TD(k,1;n).
證 設X={0,1,2,…,n-1)。K={1,2,…,n],V=K×X,(V, G, A)為一個TD(k,1;n),不失一般性,可設
G={{i}×X|i∈K}.
今由(V, G, A)構作X上的一個k×n 陣列A如下:
若{(1,a),(2,a),…,(k,a)}為 A中的一個區組。則以(a,a,…,a) 作為A中的一列,由於一個TD(k,1;n)共包含n 個區組。因此A是X上一個k×n 陣列,下面證明A是一個OA(n,1;k)。
設1≤i<j≤k,對任意x,y ∈X。由於(i,x)與(i,y)屬於 G中兩個不同的組,故必有 A中唯一的區組{(1,a),(2,a),…,(k,a)}使a=x,a=y,從而x與y在A中位於同一列,於是得到陣列A中第i行與第j行的正交性,故A為一個OA(n,1;n)。
反之。設A為X上的一個OA(n,1;k),在V=K×X上構作關聯結構D=((V, G, A),其中,
G={{i}×X|1≤i≤k}.
使對應於A中任意一列(a,a,…,a) ,在A中有一個區組{(1,a),(2,a),…,(k,a)}。如此共得n 個區組,由A中各行之間的正交性可知V中任意一對不同組的元素恰在 A的唯一的一個區組中相遇,因此 D確實是一個TD(k,1;n)。即得結論 。
引理3 TD(k,1;n)的存在性等價於RTD(k-1,1;n)的存在性 。
綜合引理1-3。便得下述定理。
定理1 設k與n為給定的正整數,k≥3,則下述命題彼此等價:
(i)存在k-2個兩兩正交的n階拉丁方;
(ii)存在正交陣列OA(n,1;k);
(iii)存在橫截設計TD(k,1;n);
(iv)存在可分解橫截設計RTD(k-1,1;n)。