簡介
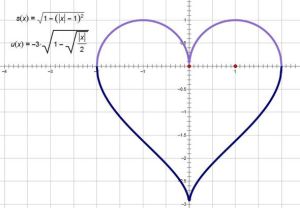 曲線
曲線 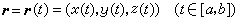 。
。
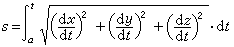
局部性質
曲線論的基本公式設正則曲線C的參數方程為r=r(s),s是弧長參數,p(s)是曲線C上參數為s即向徑為r(s)的一個定點。Q(s+Δs)為C上鄰近p的點,Q沿曲線C趨近於p時,割線pQ的極限位置稱為曲線C在p點的切線。過p點與切線垂直的平面稱為曲線C在p點的法平面。曲線C在p點的切線及C上鄰近點R確定一個平面σ,σ的極限位置稱為曲線C在p點的密切平面,它在p點的法線稱為曲線C在p點的次法線,曲線C在p點的切線和次法線決定的平面稱為曲線C在p點的從切平面。p點的法線稱為曲線C在p點的主法線。
以"·"表示關於弧長參數s的 導數,並且設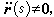 那么
那么 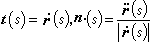 和 b(s)= t(s)× n(s)分別是曲線 C在 p(s)點的切線、主法線和次法線上的單位向量,並且 t(s)指向曲線 C的正向。 n(s)指向曲線凹入的一方。 t(s)、 n(s)和 b(s)按此順序構成 右手系,且分別稱為曲線 C在 p(s)點的切向量、主法向量和次法向量。{ r(s), t(s), n(s), b(s)}稱為曲線 C在 p(s)點的弗雷內標架。
和 b(s)= t(s)× n(s)分別是曲線 C在 p(s)點的切線、主法線和次法線上的單位向量,並且 t(s)指向曲線 C的正向。 n(s)指向曲線凹入的一方。 t(s)、 n(s)和 b(s)按此順序構成 右手系,且分別稱為曲線 C在 p(s)點的切向量、主法向量和次法向量。{ r(s), t(s), n(s), b(s)}稱為曲線 C在 p(s)點的弗雷內標架。 曲線 C的每一點都有弗雷內標架。為研究曲線上兩個鄰近點上弗雷內標架之間的變換關係,要討論 t(s)、 n(s)和 b(s)關於s的導向量,它們可由標架向量線性表出,這就是下述曲線論的基本公式(弗雷內公式):
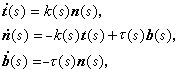
曲率曲率

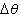 是切向量 t(s)和 t(s+Δs)之間的夾角。故曲率度量了曲線上相鄰兩點的切向量的夾角關於弧長的變化率。直線的曲率恆為0。圓周的曲率等於其半徑的 倒數。當曲線 C在 p(s)點的曲率 k≠0時,在 p(s)點的主法線上沿 n(s)的正向取點 Q,使得 pQ=1/ k,在 p點的密切平面上以 Q為中心,1/ k為半徑的圓稱為曲線 C在 p點的 曲率圓或密切圓, Q和1/ k分別稱為 曲率中心和曲率半徑。密切圓是過曲線 C上 p(s)點和鄰近兩點的圓的極限位置。
是切向量 t(s)和 t(s+Δs)之間的夾角。故曲率度量了曲線上相鄰兩點的切向量的夾角關於弧長的變化率。直線的曲率恆為0。圓周的曲率等於其半徑的 倒數。當曲線 C在 p(s)點的曲率 k≠0時,在 p(s)點的主法線上沿 n(s)的正向取點 Q,使得 pQ=1/ k,在 p點的密切平面上以 Q為中心,1/ k為半徑的圓稱為曲線 C在 p點的 曲率圓或密切圓, Q和1/ k分別稱為 曲率中心和曲率半徑。密切圓是過曲線 C上 p(s)點和鄰近兩點的圓的極限位置。 撓率撓率
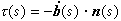 ,它的絕對值
,它的絕對值 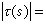
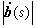 度量了曲線上鄰近兩點的次法向量之間的夾角對弧長的變化率。平面曲線是撓率恆為零的曲線。空間曲線如不是落在一平面上,則稱為撓曲線。
度量了曲線上鄰近兩點的次法向量之間的夾角對弧長的變化率。平面曲線是撓率恆為零的曲線。空間曲線如不是落在一平面上,則稱為撓曲線。 若 p 0(s 0)點的曲率和撓率均不為零,取 p 0為原點,曲線的切線、主法線和次法線為坐標軸,在 p 0附近,曲線可近似地表示為:
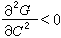
曲線的弧長s、曲率k(s)和撓率τ(s)是運動的不變數。反過來,曲線的曲率和撓率也完全決定了曲線的形態。具體地說,如果給定了兩個連續函式k(s)>0和τ(s),s∈【α,b)】,則存在以k(s)和τ(s)分別為其曲率和撓率的曲線,並且這些曲線經過空間的一個運動可以互相疊合。
特殊曲線
平面曲線撓率恆為零的曲線為平面曲線。設Oxy為歐氏平面E2 的笛卡兒直角坐標系,則平面曲線C的參數方程為r=r(s)=(x(s),y(s)),s為弧長參數,弗雷內公式可寫成
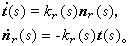
 /2。 k r(s)稱為相對曲率, k r>0和 k r0,稱為貝特朗曲線。這樣的曲線可與另一條曲線
/2。 k r(s)稱為相對曲率, k r>0和 k r0,稱為貝特朗曲線。這樣的曲線可與另一條曲線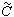 建立一一對應關係,使在對應點的主法線重合。反之,這個性質也是曲線成為貝特朗曲線的充分條件。這樣的C和
建立一一對應關係,使在對應點的主法線重合。反之,這個性質也是曲線成為貝特朗曲線的充分條件。這樣的C和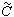 中的每一條都稱為另一條的侶線。兩條貝特朗侶線在其對應點的切線作固定角。漸縮線與漸伸線
中的每一條都稱為另一條的侶線。兩條貝特朗侶線在其對應點的切線作固定角。漸縮線與漸伸線 曲線C1的切線為另一條曲線C2的法線,則C1稱為C2的漸縮線或漸屈線,C2稱為C1的漸伸線或漸開線。可以證明與齒廓曲線為漸伸線的齒輪相嚙合的齒輪的齒廓曲線也是漸伸線,通常齒輪的齒廓曲線都採用圓的漸伸線。
整體性質
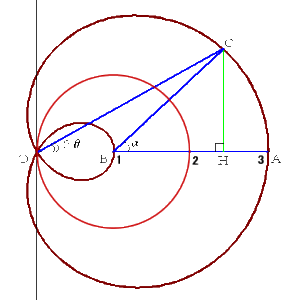 曲線
曲線 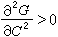
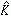 表示。正則閉曲線的全曲率等於其切線像的長度。關於正則閉曲線的全曲率的界限有下述二定理。
表示。正則閉曲線的全曲率等於其切線像的長度。關於正則閉曲線的全曲率的界限有下述二定理。 芬切爾定理正則閉曲線 C的全曲率
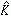 ≥2
≥2 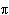 ,且等號僅當 C為平面凸閉曲線時成立。這定理給出了正則閉曲線的全曲率的下限,白正國將此定理推廣到分段光滑的閉曲線。
,且等號僅當 C為平面凸閉曲線時成立。這定理給出了正則閉曲線的全曲率的下限,白正國將此定理推廣到分段光滑的閉曲線。 法里-米爾諾定理簡單正則有結空間閉曲線的全曲率
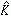 >4
>4 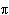 。
。 閉曲線 C的撓率 τ(s)沿自身的積分
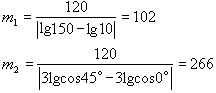
設 C為平面正則閉曲線,則當點繞 C一周時,曲線 C的切線像 t(s)將在單位圓周上繞若干圈,這個圈數 i r(以逆時針向環繞時圈數為正,順時針向時為負)稱為 C的旋轉指標,可算得
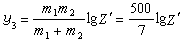 ,
,
將平面上一條定長的細繩首尾相接而構成一條簡單閉曲線,它把平面分成以其為 公共邊界的二個部分,它所圍成的區域的面積為最大時,其形狀是圓周。有如下更精確的結論:設曲線 C是長度為 L的平面正則簡單閉曲線, A是 C所圍區域的面積,那么 L 2 -4
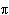 A≥0,並且等號若且唯若 C是圓周時成立。上述不等式有過種種的推廣,這類問題叫做等周問題。對於平面曲線,與空間曲線論基本定理相仿,它的形態由其相對曲率 k r(s)所確定,故 k r(s)的極值自然是令人感興趣的。相對曲率 k r(s)的逗留點,即
A≥0,並且等號若且唯若 C是圓周時成立。上述不等式有過種種的推廣,這類問題叫做等周問題。對於平面曲線,與空間曲線論基本定理相仿,它的形態由其相對曲率 k r(s)所確定,故 k r(s)的極值自然是令人感興趣的。相對曲率 k r(s)的逗留點,即 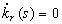 的點稱為曲線的頂點,對於凸閉曲線,即位於其上每一點的切線的一側的曲線,成立著名的四頂點定理:平面凸閉曲線至少有四個頂點,因為橢圓只有四個頂點,所以這個結論不能再改進。此外,還可以利用柯西-克羅夫頓公式來計算平面正則曲線的長度(見 積分幾何學)。
的點稱為曲線的頂點,對於凸閉曲線,即位於其上每一點的切線的一側的曲線,成立著名的四頂點定理:平面凸閉曲線至少有四個頂點,因為橢圓只有四個頂點,所以這個結論不能再改進。此外,還可以利用柯西-克羅夫頓公式來計算平面正則曲線的長度(見 積分幾何學)。 
