次法線

點的運動學中，描述和分析點得運動方法(即自然法)中的一幾何直線，也是自然軸b所在直線。也稱副法線。 設質點沿著某一空間曲線MN運動，在軌道MN上的任意點P作密切平面，在密切平面內過P點作切線τ和法線n，再作直線b，使三者的方向關係為即互相垂直，則b稱為次法線。

自然法

利用點的運動軌跡建立弧坐標及自然軸系，並用它們來描述和分析點的運動的方法稱為 自然法。

弧坐標

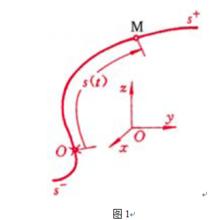
設動點 M的軌跡為如圖1所示的曲線，則動點 M在軌跡上的位置可以這樣確定：在軌跡上任選一點 O為參考點，並設點 O的某一側為正向，動點 M在軌跡上的位置由弧長確定，視弧長 s為代數量，稱它為動點 M在軌跡上的弧坐標。當動點在 M運動時， s隨時間變化，它是時間的單值連續函式，即

s=f(t) (1-1)

弧坐標示意圖

上式稱為點沿軌跡的運動方程，或以弧坐標表示的點的運動方程。如果已知點的運動方程式(1-1)，可以確定任一瞬時點的弧坐標s的值，也就確定了該瞬時動點在軌跡上的位置。

自然軸系

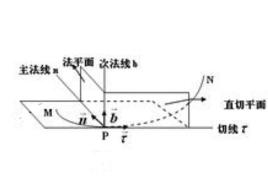
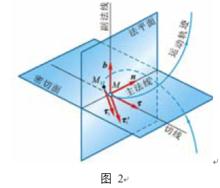
在點的運動軌跡曲線上取極為接近的兩點 M和 M，其間的弧長為△ s，這兩點的切線的單位矢量分別是 τ和 τ，其指向與弧坐標正向一致，如圖2所示。將 τ平移至點 M，則此平面趨近於某一極限位置，此極限平面稱為曲線在點 M的 密切面。過點 M並與切線垂直的平面稱為 法平面，法平面與密切面的交線稱為 主法線。令主法線的單位矢量為 n，指向曲線內凹一側。過點 M且垂直於切線及主法線的直線稱 副法線(次法線)，其單位矢量 b，指向與 τ， n構成右手系，即

b= τ× n

以點M為原點，以切線、主法線和副法線為坐標軸組成的正交坐標系稱為曲線在點M的 自然坐標系，這三個軸稱為 自然軸。注意，隨著點M在軌跡上運動， τ， n， b的方向也在不斷變動；自然坐標系是沿曲線而變動的遊動坐標系。

自然軸系示意圖