簡介
撓率,它的絕對值度量了曲線上鄰近兩點的次法向量之間的夾角對弧長的變化率。平面曲線是撓率恆為零的曲線。空間曲線如不是落在一平面上,則稱為撓曲線。
在三維曲線的基本微分幾何中,曲線的撓率代表曲率平面的扭曲程度。 總之,空間曲線的曲率和扭轉類似於平面曲線的曲率。 舉個例子,它們是由Frenet-Serret公式給出的Frenet框架的微分方程系統中的係數。
定義
令C為弧長s和單位切線向量t參數化的空間曲線。 如果在某一點的C的曲率k不為零,那么該主點法線向量和該二次正交向量是單位向量。
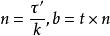 撓率
撓率τ測量給定點上的雙向正矢量的鏇轉速度。 從等式可以看出
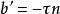 撓率
撓率這意味著
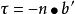 撓率
撓率備註:二次向量的導數與二次正交和正切相垂直,因此必須與主法向量成正比。 負號只是一個慣例:它是這個主題的歷史發展的產物。
通常由σ表示的扭轉半徑定義為
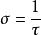 撓率
撓率幾何相關性:τ(s)測量二次正交向量的周轉。 扭轉越大,雙正則向量圍繞由切線向量給出的軸鏇轉越快(參見圖示)。 在動畫圖中,雙向正矢量的鏇轉在扭轉函式的峰值處是清晰可見的。
屬性
(1)具有非零曲率的平面曲線在所有點都具有零扭轉。 相反,如果具有非零曲率的規則曲線的扭轉相同為零,則該曲線屬於固定平面。
(2)螺鏇的曲率和扭轉是恆定的。 相反,曲率和撓率都是常數和非零的任何空間曲線都是螺鏇線。 右鏇螺鏇的撓率是正的,對於左手螺鏇是負的。
說明
令r = r(t)為空間曲線的參數方程。 假設這是一個規則參數化,並且曲線的曲率不會消失。 r(t)是t的三次微分函式,其中R3和向量中的值都是
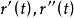 撓率
撓率並且它們是線性獨立的。
那么撓率可以由下列公式計算:
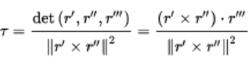 撓率
撓率對於r =(x,y,z),分量中的公式為
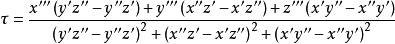 撓率
撓率撓率和曲率的區別
曲率是彎曲,撓率是扭曲。對一條平面曲線,主法向量是在平面上,與切向量垂直。次法向量等於切向量叉乘主法向量,與平面垂直。由於平面曲線的次法向量處處與平面垂直,所以平面曲線撓率處處為零。也就是發生彎曲,不扭曲。而對於三維曲線,某一點曲率,撓率都不為零,同時發生彎曲和扭曲。上面講的是三維空間中曲線的撓率。曲面的曲率,撓率可類推。至於更高維的撓率(包括曲率),則要用到微分幾何。
