曲率圓

在點處的曲線的法線上，在凹的一側取一點 ，使以O為圓心，R為半徑作圓，這個圓叫做曲線在點處的曲率圓。曲率圓方程的表達式：(x-α)^2+(y-β)^2=R^2,其中R是曲線y=f(x)在P(x0,y0)點處的曲率半徑，圓心(α,β)稱為曲線y=f(x)在P(x0,y0)點處的曲率中心。

基本信息

• 中文名稱：曲率圓
• 套用學科：數學

• 定義：以O為圓心，R為半徑作圓
• 結論：曲率半徑愈小，曲線彎曲愈甚
• 公式：(x-α)^2+(x-β)^2=R^2

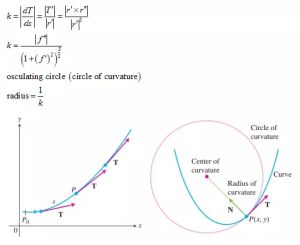
概述

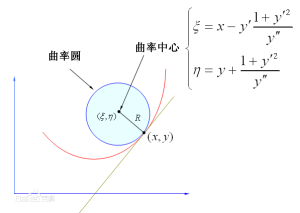曲率圓

在點處的曲線的法線上，在凹的一側取一點，使以O為圓心，R為半徑作圓，這個圓叫做曲線在點處的曲率圓。
記：R為曲率半徑
以平面曲線為例。作一圓通過平面曲線上的某一點A和鄰近的另外兩點B1和B2，當B1和B2無限趨近於A點時，此圓的極限位置叫做曲線A點處的曲率圓。曲率圓的中心和半徑分別稱為曲線在A點的曲率中心（centreofcurvature）和曲率半徑（radiasofcurvature）。曲率半徑愈小，表示曲線彎曲愈甚。
曲率圓方程的表達式：(x-α)^2+(x-β)^2=R^2,其中R是曲線y=f(x)在P(x0,y0)點處的曲率半徑，圓心(α,β)稱為曲線y=f(x)在P(x0,y0)點處的曲率中心 ，且α=x0-f'(x0){1+[f'(x0)]^2}/f''(x0),β=y0+{1+[f'(x0)]^2}/f''(x0).

相關

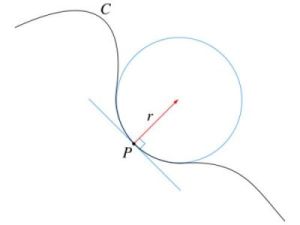使以O為圓心，R為半徑作圓，這個圓叫做曲線在點處的曲率圓

曲率圓