簡介
用來檢驗觀測數與依照某種假設或分布模型計算得到的理論數之間一致性的一種統計假設檢驗，以便判斷該假設或模型是否與實際觀測數相吻合。
分類
（1）吻合度檢驗：檢驗觀測數與理論數之間的一致性。
（2）獨立性檢驗：通過檢驗觀測數與理論數之間的一致性來判斷事件之間的獨立性。
步驟
（1）將觀測值分為k組 ；
（2）計算n次觀測值中每組的觀測頻數，記為Oi；
（3）根據變數的分布規律或機率運算法則，計算每組的理論頻率為Pi；
（4）計算每組的理論頻數Ti ；
（5）檢驗Oi與Ti的差異顯著性，判斷兩者之間的不符合度
a、零假設：H0：O-T=0；備擇假設： O-T≠0（這裡檢驗的不是參數，而是判斷觀測數是否符合理論分布）
b、檢驗統計量：這裡要求n充分的大，當n≥50時（最好≥100），所定義的檢驗統計量近似服從卡方分布，Ti=nPi不得小於5，若小於5，將尾區相鄰的組合併，直到合併後的組的Ti≥5，合併後再計算卡方值。
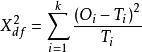擬合優度檢驗c、建立拒絕域
d、作出統計學結論
獨立性檢驗
原理
通過觀測數與理論數之間的一致性判斷事件之間的獨立性，即判斷兩個事件是否是獨立事件或處理間差異是否顯著。
方法
將數據列成列聯表，也稱列聯表卡方檢驗。
步驟
（1）提出假設 H0：O-T=0；HA： O-T≠0；
（2）根據機率的乘法法則計算理論數：理論數的計算方法；
（3）檢驗統計量；
（4）確定自由度： 2×2列聯表的自由度df=(r-1)(c-1)，r是列聯表的行數，c是列聯表的列數，若自由度=1，則應做連續性校正；
（5）拒絕域的建立；
（6）結論
