簡介
相關關係是一種非確定性的關係,例如,以X和Y分別記一個人的身高和體重,或分別記每公頃施肥量與每公頃小麥產量,則X與Y顯然有關係,而又沒有確切到可由其中的一個去精確地決定另一個的程度,這就是相關關係。
分類
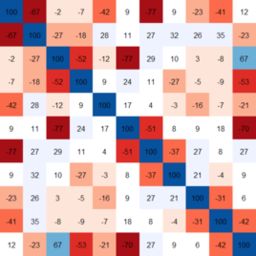
1、線性相關分析:研究兩個變數間線性關係的程度。用相關係數r來描述。
(1)正相關:如果x,y變化的方向一致,如身高與體重的關係,r>0;一般地,
·|r|>0.95 存在顯著性相關;
·|r|≥0.8 高度相關;
·0.5≤|r|<0.8 中度相關;
·0.3≤|r|<0.5 低度相關;
·|r|<0.3 關係極弱,認為不相關
(2)負相關:如果x,y變化的方向相反,如吸菸與肺功能的關係,r<0;
(3)無線性相關:r=0。
如果變數Y與X間是函式關係,則r=1或r=-1;如果變數Y與X間是統計關係,則-1<1。
(4)r的計算有三種:
①Pearson相關係數:對定距連續變數的數據進行計算。
②Spearman和Kendall相關係數:對分類變數的數據或變數值的分布明顯非正態或分布不明時,計算時先對離散數據進行排序或對定距變數值排(求)秩。
2、偏相關分析:研究兩個變數之間的線性相關關係時,控制可能對其產生影響的變數。如控制年齡和工作經驗的影響,估計工資收入與受教育水平之間的相關關係。
3、距離分析:是對觀測量之間或變數之間相似或不相似程度的一種測度,是一種廣義的距離。分為觀測量之間距離分析和變數之間距離分析。
(1)不相似性測度:
·a、對等間隔(定距)數據的不相似性(距離)測度可以使用的統計量有Euclid歐氏距離、歐氏距離平方等。
·b、對計數數據使用卡方。
·c、對二值(只有兩種取值)數據,使用歐氏距離、歐氏距離平方、尺寸差異、模式差異、方差等。
(2) 相似性測度:
·a、等間隔數據使用統計量Pearson相關或餘弦。
·b、測度二元數據的相似性使用的統計量有20餘種。
相關關係
相關分析與回歸分析在實際套用中有密切關係。然而在回歸分析中,所關心的是一個隨機變數Y對另一個(或一組)隨機變數X的依賴關係的函式形式。而在相關分析中 ,所討論的變數的地位一樣,分析側重於隨機變數之間的種種相關特徵。例如,以X、Y分別記小學生的數學與語文成績,感興趣的是二者的關係如何,而不在於由X去預測Y。
復相關
研究一個變數 x0與另一組變數 (x1,x2,…,xn)之間的相關程度。例如,職業聲望同時受到一系列因素(收入、文化、權力……)的影響,那么這一系列因素的總和與職業聲望之間的關係,就是復相關。復相關係數R0.12…n的測定,可先求出 x0對一組變數x1,x2,…,xn的回歸直線,再計算x0與用回歸直線估計值憫之間的簡單直線回歸。復相關係數為
R0.12…n的取值範圍為0≤R0.12…n≤1。復相關係數值愈大,變數間的關係愈密切。
偏相關
研究在多變數的情況下,當控制其他變數影響後,兩個變數間的直線相關程度。又稱淨相關或部分相關。例如,偏相關係數 r13.2表示控制變數x2的影響之後,變數 x1和變數x3之間的直線相關。偏相關係數較簡單直線相關係數更能真實反映兩變數間的聯繫。
偏相關係數、復相關係數、簡單直線相關係數之間存在著一定的關係。以3個變數x1,x2,x3為例,它們有如下的關係:
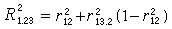 公式
公式或
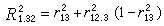 公式
公式定序變數
討論兩個定序變數間的相關的程度與方向。又稱等級相關。例如,研究夫婦雙方文化程度的相關等。等級相關係數有R係數和γ係數。
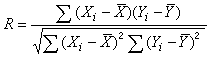 公式
公式R係數 計算方法與簡單直線相關係數相同。 式中
X,Y分別為x,y的測量值的等級。
英國統計學家 C.E.斯皮爾曼從R係數中推導出簡捷式,稱斯皮爾曼等級相關係數:
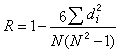 公式
公式式中di=xi-yi,i=1,2,…,N(N為次數)。
等級相關係數 R具有與簡單直線相關相同的性質:取值範圍在〔-1,+1〕之間;R的絕對值愈大,變數間的等級相關程度愈大。
γ係數 適用於資料次數N 很大的情況。
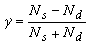 公式
公式式中Ns為同序對數目,Nd為異序對數目。
同序對表示兩個個案(xi,yi)和(xj,yj)相比時,具有xi>xj,則yi>yj的性質;反之,若xi>xj,但yi
γ係數的取值範圍在〔-1,+1〕之間。γ的絕對值愈大,變數間的等級相關程度愈大。