表達式
多元線性回歸模型的一般形式為
Yi=β0+β1X1i+β2X2i+…+βkXki+μi i=1,2,…,n
其中 k為解釋變數的數目，βj（j=1,2,…,k)稱為回歸係數（regression coefficient)。上式也被稱為總體回歸函式的隨機表達式。它的非隨機表達式為
E(Y∣X1i,X2i,…Xki,)=β0+β1X1i+β2X2i+…+βkXki
βj也被稱為偏回歸係數（partial regression coefficient)
計算模型
一元線性回歸是一個主要影響因素作為自變數來解釋因變數的變化，在現實問題研究中，因變數的變化往往受幾個重要因素的影響，此時就需要用兩個或兩個以上的影響因素作為自變數來解釋因變數的變化，這就是多元回歸亦稱多重回歸。當多個自變數與因變數之間是線性關係時，所進行的回歸分析就是多元性回歸。 設y為因變數X1,X2…Xk為自變數，並且自變數與因變數之間為線性關係時，則多元線性回歸模型為：
Y=b0+b1x1+…+bkxk+e
其中， b0為常數項，b1,b2…bk為回歸係數， b1為X1,X2…Xk固定時， x1每增加一個單位對y的效應，即 x1對y的偏回歸係數；同理 b2為X1,X2…Xk固定時， x2每增加一個單位對y的效應，即， x2對y的偏回歸係數，等等。如果兩個自變數 x1, x2同一個因變數y呈線相關時，可用二元線性回歸模型描述為：
y= b0 + b1 x1 + b2 x2 + e
建立多元線性回歸模型時，為了保證回歸模型具有優良的解釋能力和預測效果，應首先注意自變數的選擇，其準則是：
(1)自變數對因變數必須有顯著的影響，並呈密切的線性相關；
(2)自變數與因變數之間的線性相關必須是真實的，而不是形式上的；
(3)自變數之間應具有一定的互斥性，即自變數之間的相關程度不應高於自變數與因變數之因的相關程度；
(4)自變數應具有完整的統計數據，其預測值容易確定。
多元性回歸模型的參數估計，同一元線性回歸方程一樣，也是在要求誤差平方和（Σe)為最小的前提下，用最小二乘法求解參數。以二線性回歸模型為例，求解回歸參數的標準方程組為
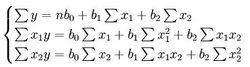多元線性回歸模型解此方程可求得 b0, b1, b2的數值。亦可用下列矩陣法求得
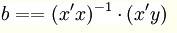多元線性回歸模型即
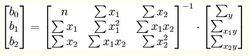多元線性回歸模型