基本介紹
利用觀測數據判斷總體是否服從常態分配的檢驗稱為正態性檢驗,它是統計判決中重要的一種特殊的擬合優度假設檢驗。常用的正態性檢驗方法有正態機率紙法、夏皮羅維爾克檢驗法(Shapiro-Wilktest),科爾莫戈羅夫檢驗法,偏度-峰度檢驗法等。
正態性檢驗問題為
 正態性檢驗
正態性檢驗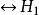 正態性檢驗
正態性檢驗: 總體服從常態分配 : 總體不服從常態分配。
在正態性檢驗中,偏度峰度正態性檢驗統計量原理清晰、計算
簡單,通常被首選用來作為正態性檢驗統計量。
檢驗特點
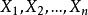 正態性檢驗
正態性檢驗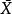 正態性檢驗
正態性檢驗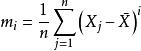 正態性檢驗
正態性檢驗設 。表示來自總體的樣本, 表示樣本均值, 表示 i 階樣本中心矩。常態分配的偏度和峰度均為 0,其中偏度和峰度的定義分別為
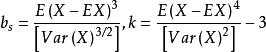 正態性檢驗
正態性檢驗該檢驗就是根據這個特點來檢驗分布正態性的。
檢驗方法
偏度-峰度正態性檢驗包括下面三種方法:
偏度檢驗
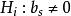 正態性檢驗
正態性檢驗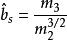 正態性檢驗
正態性檢驗使用偏度檢驗時,總體具有僅在偏度方向上偏離正態的先驗信息。因而備擇假設為 。檢驗統計量為 。
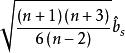 正態性檢驗
正態性檢驗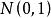 正態性檢驗
正態性檢驗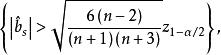 正態性檢驗
正態性檢驗當總體服從常態分配時, 的極限分布是 ,因此水平為 α檢驗的拒絕域為 這裡是標準常態分配的分位數。
峰度檢驗
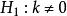 正態性檢驗
正態性檢驗使用峰度檢驗時,總體具有僅在峰度方向上偏離正態的先驗信息。因而備擇假設為 。檢驗的統計量為
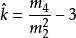 正態性檢驗
正態性檢驗。
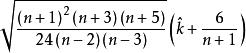 正態性檢驗
正態性檢驗 正態性檢驗
正態性檢驗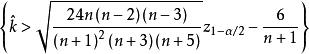 正態性檢驗
正態性檢驗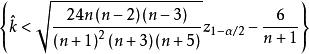 正態性檢驗
正態性檢驗當總體服從常態分配時 的極限分布是 ,因此水平為α檢驗的拒絕域為 或 。
偏度和峰度聯合檢驗
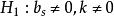 正態性檢驗
正態性檢驗使用聯合檢驗的條件為: 總體具有在偏度和峰度方向上都偏離正態的先驗信息,它的備擇假設為 。首先計算統計量
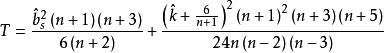 正態性檢驗
正態性檢驗 正態性檢驗
正態性檢驗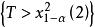 正態性檢驗
正態性檢驗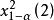 正態性檢驗
正態性檢驗 正態性檢驗
正態性檢驗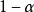 正態性檢驗
正態性檢驗的值,然後根據該統計量的極限分布自由度是2 的 分布,所以水平為 α檢驗的拒絕域是 ,其中 是自由度是2的 分布的 分位數。
變數相關
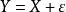 正態性檢驗
正態性檢驗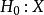 正態性檢驗
正態性檢驗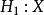 正態性檢驗
正態性檢驗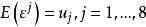 正態性檢驗
正態性檢驗考慮變數X 帶有測量誤差模型 的正態性檢驗問題, 服從常態分配 不服從常態分配,其中 已知。
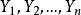 正態性檢驗
正態性檢驗設 是來自上述模型的一組樣本,則給出變數X 的偏度-峰度正態性檢驗統計量的定義如下:
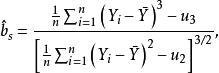 正態性檢驗
正態性檢驗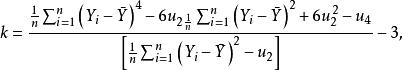 正態性檢驗
正態性檢驗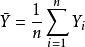 正態性檢驗
正態性檢驗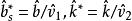 正態性檢驗
正態性檢驗這裡 。變數 X 的標準化偏度和峰度檢驗統計量分別定義為: ,其中
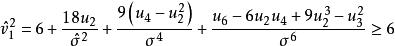 正態性檢驗
正態性檢驗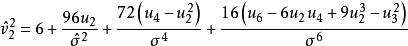 正態性檢驗
正態性檢驗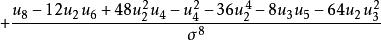 正態性檢驗
正態性檢驗≥ 24,
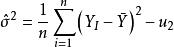 正態性檢驗
正態性檢驗偏度檢驗
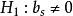 正態性檢驗
正態性檢驗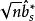 正態性檢驗
正態性檢驗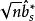 正態性檢驗
正態性檢驗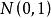 正態性檢驗
正態性檢驗 正態性檢驗
正態性檢驗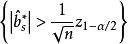 正態性檢驗
正態性檢驗使用偏度檢驗時,總體具有僅在偏度方向上偏離正態的先驗信息。因而備擇假設為 。檢驗統計量為 。當總體服從常態分配時, 的極限分布是 ,因此水平為 檢驗的拒絕域為 。
峰度檢驗
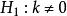 正態性檢驗
正態性檢驗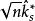 正態性檢驗
正態性檢驗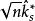 正態性檢驗
正態性檢驗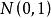 正態性檢驗
正態性檢驗 正態性檢驗
正態性檢驗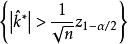 正態性檢驗
正態性檢驗使用峰度檢驗時,總體具有僅在峰度方向上偏離正態的先驗信息。因而備擇假設為 。檢驗的統計量為 當總體服從常態分配時, 的極限分布是 ,因此水平為 檢驗的拒絕域為 。
偏度和峰度聯合檢驗
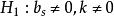 正態性檢驗
正態性檢驗使用聯合檢驗的條件為: 總體具有在偏度和峰度方向上都偏離正態的先驗信息,它的備擇假設為: ,首先計算統計量
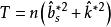 正態性檢驗
正態性檢驗 正態性檢驗
正態性檢驗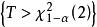 正態性檢驗
正態性檢驗的值,然後根據該統計量的極限分布自由度是 2 的 分布,所以拒絕域是 。
在一定的條件下,這些偏度和峰度檢驗統計量具有漸近正態的優良性質和良好的功效。
圖形中的垂直尺度類似於正態機率圖中的垂直尺度。水平軸為線性尺度。此線形成數據所來自總體的累積分布函式的估計值。圖中會顯示總體參數的數字估計(Xbar和 s)、正態性檢驗值以及關聯的p 值。

