張角公式:公元467年,中國的朱謙發現了張角定理。
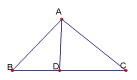 張角公式
張角公式公式:
在△ABC中,D是BC上的一點。連結AD。張角定理指出:sin∠BAD/AC+sin∠CAD/AB=sin∠BAC/AD
逆定理如果sin∠BAD/AC+sin∠CAD/AB=sin∠BAC/AD,那么B,D,C三點共線。
張角定理的推論
在定理的條件下,且∠BAD=∠CAD,即AD平分∠BAC,則BDC共線的充要條件是:2cos∠BAD/AD=1/AB+1/AC證明:
設∠1=∠BAD,∠2=∠CAD
由分角定理,
S△ABD/S△ABC=BD/BC=(AD/AC)*(sin∠1/sin∠BAC)
→(BD/BC)*(sin∠BAC/AD)=sin∠1/AC(1.1)
S△ACD/S△ABC=CD/BC=(AD/AB)*(sin∠2/sin∠BAC)
→(CD/BC)*(sin∠BAC/AD)=sin∠2/AB(1.2)
(1.1)式+(1.2)式得sin∠1/AC+sin∠2/AB=sin∠BAC/AD
張角定理的套用
把平面幾何和三角函式緊密相連,它給出了用三角法處理平面幾何問題的一個頗為有用的公式,並且是一個非常有效的證明三點共線的手段。用它去解幾何題,適當地配合三角形面積公式、正弦定理、三角公式、幾何知識,可以大大簡化解題步驟,眾多的幾何問題可以得到簡捷統一的解決
參考資料:
1.湖南師範大學出版社《奧賽經典-奧林匹克數學中的幾何問題》(沈文選張垚冷崗松編著)
