數學定理
定義
帕斯卡定理指圓錐曲線內接六邊形其三對邊的交點共線，與布列安桑定理對偶，是帕普斯定理的推廣。該定理由法國數學家布萊士·帕斯卡於16歲時提出，是射影幾何中的一個重要定理。
定義的推廣
本定理可推廣為：圓錐曲線內接六邊形的三雙對邊(所在直線)的交點共線。
證明
可以利用射影變換，將圓錐曲線的命題轉化為圓的命題。現在只需要證明圓的內接六邊形ABCDEF三雙對邊的交點共線即可。
帕斯卡定理的證法有許多種，在此只列舉三種：
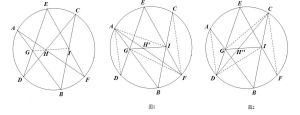面積法
，即證：
共邊定理+共角定理可得：(注:S-AGF表示△AGF的面積)
命題得證
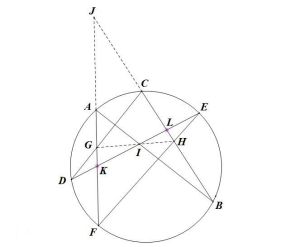梅涅勞斯定理證法
三式相乘得：
......(1)圓冪定理得：
將三式代入(1)得：
梅涅勞斯逆定理得：G、I、H共線，命題得證
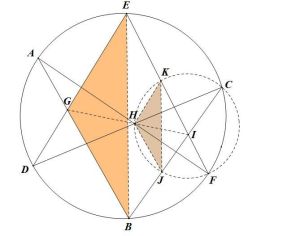位似證法物理定理
定義
帕斯卡定律：加在密閉液體任一部分的壓強，必然按其原來的大小，由液體向各個方向傳遞。
原理的發現
發現定理 1651~1654年，帕斯卡研究了液體靜力學和空氣的重力的各種效應。
經過數年的觀察、實驗和思考，綜合成《論液體的平衡和空氣的重力》一書。提出了著名的帕斯卡定律（或稱帕斯卡原理），即加在密閉液體任何一部分上的壓強，必然按照其原來的大小由液體向各個方向傳遞。
原理的意義
著名科學史家沃爾夫稱，帕斯卡的這一發現是17世紀力學發展的一個重要里程碑。
帕斯卡在此書中詳細討論了液體壓強問題。在第一章中，帕斯卡敘述了幾種實驗，它們的結果表明，任何水柱，不論直立或傾斜，也不論其截面積的大小，只要豎直高度相同，則施加於水柱底部的某一已知面積的活塞上的力也相同。這一個力實際上是液體所受的重力。書中詳細敘述了密封容器中的流體能傳遞壓強，討論了連通器的原理。
帕斯卡利用一個充水的容器，它有兩個圓筒形的出口，除此之外，其他部分都封閉。兩個出口的截面積相差100倍，在每一個出口的圓筒中放入一個大小剛好適合的活塞，則小活塞上一個人施加的推力等於大活塞上100人所施加的推力，因而可以勝過大活塞上99個人施加的推力，不管這兩個出口大小的比例如何，只要施加於兩個活塞上的力和兩個出口的大小成比例，則水的平衡就可以實現。帕斯卡在書中一一敘述了密閉液體、壓強不變、向各方傳遞等帕斯卡定律的基本點。
定律的發現
此書是帕斯卡於1653年寫成的，但直到他逝世後的第二年----1663年才首次面世。帕斯卡是在大量觀察、實驗的基礎上，又用虛功原理加以證明才發現了帕斯卡定律的。在帕斯卡做過的大量實驗中，最著名的一個是這樣的：他用一個木酒桶，頂端開一個孔，孔中插接一根很長的鐵管子，將接插口密封好。實驗的時候，酒桶中先灌滿水，然後慢慢地往鐵管子裡注幾杯水，當管子中的水柱高達幾米的時候，就見木桶突然破裂，水從裂縫中向四面八方噴出。帕斯卡定律的發現，為流體靜力學的建立奠定了基礎。
發展
帕斯卡還在這一定律的基礎上提出了連通器的原理和後來得到廣泛套用的水壓機的最初構想。他又指出器壁上所受的、由於液體重力而產生的壓強，僅僅與深度有關；他用實驗，並從理論上解釋了與此有關的液體靜力學佯謬現象。他在一周之內就突擊讀完了歐幾里得《幾何原本》的前六本，並還能把它套用於力學。1653年，他進入牛津大學裡奧爾學院做工讀生。他沒有取得學士學位，而是在1663年獲得文學碩士學位。
套用
帕斯卡定律是流體（氣體或液體）力學中，指封閉容器中的靜止流體的某一部分發生的壓強變化，將毫無損失地傳遞至流體的各個部分和容器壁。帕斯卡首先闡述了此定律。壓強等於作用力除以作用面積。根據帕斯卡原理，在水力系統中的一個活塞上施加一定的壓強，必將在另一個活塞上產生相同的壓強增量。如果第二個活塞的面積是第一個活塞的面積的10倍，那么作用於第二個活塞上的力將增大為第一個活塞的10倍，而兩個活塞上的壓強仍然相等。水壓機就是帕斯卡原理的實例。它具有多種用途，如液壓制動等。
帕斯卡還發現：靜止流體中任一點的壓強各向相等，即該點在通過它的所有平面上的壓強都相等。這一事實也稱作帕斯卡原理（定律）。
