公式
定義式：p=F/S，液體壓強公式推導過程：要想得到液面下某處的壓強，可以構想這裡有一個水平放置的“平面”，這個平面以上的液柱對平面的壓力等於液柱所受的重力。這個平面上方的液柱對平面的壓力F=G=mg=ρVg=ρShg，平面受到的壓強，p=F/S=G/S=mg/S=ρVg/S=ρShg/S=ρgh（適用於液體）
單位
“p”是指壓強（注意：是小寫的“p”，而不是大寫的“P”，大寫“P”是指做功的功率）單位是“帕斯卡”，簡稱“帕”，符號是“Pa”。F表示力，單位是“牛頓”，簡稱“牛”，符號是“N”。S表示受力面積，單位是“平方米”，符號是“㎡”。
簡介
壓強與力和受力面積的關係為：
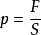壓強其中:
p代表壓強
F代表垂直作用力（壓力）
S代表受力面積
根據上述公式，可以推導出如下的公式：
該公式是用於計算液體的壓強，其中：
p表示壓強
ρ表示液體的密度
g≈9.8N/kg且在數值上等於重力加速度
h表示液體的深度
壓強| 壓強 | ||
| 公式 | p=F/S | p=ρgh |
| 適用範圍 | 通用公式：柱形物體 | 一般液體 |
| 一般思路 | 水平面：F=Sp | 先p=ρgh再F=PS |
| 特殊思路 | 圓柱形物體p=ρgh | 規則容器裝液體：F=G p=F/S |
實驗
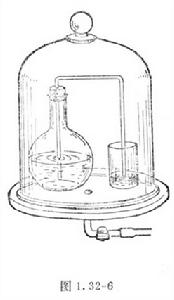
馬德堡半球實驗
馬德堡半球實驗圖1654年5月8日，馬德堡市有一大批人圍在實驗場上。有的說這樣，有的說那樣，有的支持格里克市長，希望實驗成功；有的斷言實驗會失敗；人們在議論著，在爭論著；在預言著；格里克和助手當眾把這個黃銅的半球殼中間墊上橡皮圈；再把兩個半球殼灌滿水後合在一起；然後把水全部抽出，使球內形成真空；最後，把氣嘴上
的龍頭擰緊封閉。這時，周圍的大氣把兩個半球緊緊地壓在一起。格里克一揮手，四個馬夫牽來八匹高頭大馬，在球的兩邊各拴四匹．格里克一聲令下，四個馬夫揚鞭催馬、背道而拉！好像在“拔河”似的。
實驗半球4個馬夫，8匹大馬，都搞得渾身是汗。但是，銅球仍是原封不動．格里克只好搖搖手暫停一下。然後，左右兩隊，人馬倍增。馬夫們喝了些開水，擦擦頭額上的汗水，又在準備著第二次表現。格里克再一揮手，實驗場上更是熱鬧非常。16匹大馬，拚命地拉，八個馬夫在大聲吆喊，揮鞭催馬……來看實驗的人群，更是伸長脖子，一個勁兒地看著，不時地發出“嘩！嘩！”的響聲。突然，“啪！”的一聲巨響，銅球分開成原來的兩半，格里克舉起這兩個重重的半球自豪地向大家高聲宣告：“女士們！先生們！你們該相信了吧！大氣壓是有的，大氣壓力是大得這樣厲害！這么驚人！……”實驗結束後，仍有些人不理解這兩個半球為什麼拉不開，七嘴八舌地問他，他又耐心地作著詳盡的解釋：“平時，我們將兩個半球緊密合攏，無須用力，就會分開．這是因為球內球外都有大氣壓力的作用；相互抵消平衡了。好像沒有大氣作用似的。今天，我把它抽成真空後，球內沒有向外的大氣壓力了，只有球外大氣緊緊地壓住這兩個半球……”。
通過這次“大型實驗”，人們都終於相信有真空；有大氣；大氣有壓力；大氣壓很驚人，但是，為了這次實驗，格里克市長竟花費了4千英鎊。
實驗意義：第一次證明了有大氣壓的存在，而且很大。
帕斯卡裂桶實驗
帕斯卡在1648年表演了一個著名的實驗：他用一個密閉的裝滿水的桶，在桶蓋上插入一根細長的管子，從樓房的陽台上向細管子裡灌水。結果只用了一杯水，就把桶壓裂了，桶里的水就從裂縫中流了出來。原來由於細管子的容積較小，一杯水灌進去，其深度也是很大的。這就是歷史上有名的帕斯卡桶裂實驗。 一個容器里的液體，對容器底部（或側壁）產生的壓力遠大於液體自身的重力，這對許多人來說是不可思議的。
改進
該實驗裝置高度太高不便在教室里演示，可啟發學生思考：能否把所有的裝置都相應地縮小呢？答案是否定的。接著再問：管長減小了，液體壓強減小了，液體對木桶的壓力必定減小；而桶儘管縮小了，但其耐壓性幾乎不變，桶就不可能裂開，能否用其它物體來模擬“裂桶”呢？學生自然會想到用耐壓性較低的物體來代替（如薄塑膠袋）。比較裝滿水的塑膠袋在同質量的一杯水與一管水作用下不同情形，液體壓強的實質就非常容易理解了。
取一個演示液體測壓強用的大廣口瓶（直徑約30厘米，高約40厘米），在瓶下部的側壁管口用橡皮薄膜紮緊密封，將紅色的水從瓶口倒入，隨著瓶中水位的升高，側管的橡皮薄膜漸漸鼓出，可以看到，即使灌滿水後，薄膜鼓出的程度也並不十分明顯。這說明雖然瓶中裝了很多很重的水，但對側壁的壓強並不很大。再取一根1米長的托里拆利玻璃管，通過打有小孔的瓶塞插入大瓶中，並把塞塞緊密封。讓一個學生站到凳子上將燒杯中的水用漏斗漸漸灌入管中，當玻璃管中紅色水升高50厘米以上時，只見大瓶側管的橡皮薄膜大幅度鼓出，現象生動明顯。
因為液體的壓強等於密度、深度和重力加速度常數之積。在這個實驗中，水的密度不變，但深度一再增加，則下部的壓強越來越大，其液壓終於超過木桶能夠承受的上限，木桶隨之裂開。
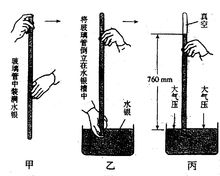托里拆利實驗帕斯卡“桶裂”實驗可以很好地證明
液體壓強與液體的深度有關，而與液體的質量無關。
托里拆利實驗
托里拆利實驗測出了大氣壓強的具體數值。在長約1m、一端封閉的玻璃管里灌滿水銀，將管口堵住，然後倒插在水銀槽中（保持垂直），放開堵管口的手指時，管內水銀面下降一些就不再下降，這時管內外水銀面的高度差為760mm。
管內留有760mm高水銀柱的原因正是因為有大氣壓的存在。由液體壓強的特點可知，水銀槽內液體表面的壓強與玻璃管內760毫米水銀柱下等高處的壓強應是相等的。水銀槽液體表面的壓強為大氣壓強，由於玻璃管內水銀柱上方是真空的，受不到大氣壓力的作用，管內的壓強只能由760mm高的水銀柱產生。因此，大氣壓強與760毫米高水銀產生的壓強相等。
通常情況下，表示氣體壓強的常用單位有帕斯卡、毫米水銀柱（毫米汞柱）、厘米水銀柱（厘米汞柱）、標準大氣壓，它們的符號分別是Pa、mmHg、cmHg、Atm。
大氣壓強
大氣壓的存在
【例1】用吸管吸飲料
【例2】吸盤貼在光滑的牆壁上不脫落
產生原因
空氣受到重力作用，而且空氣具有流動性，因此空氣內部向各個方向都有壓強，這個壓強就叫大氣壓強。
發現
大氣壓強17世紀，德國馬德堡市有一位市長，名叫奧托·馮格里克．他是個博學多才的軍人，喜歡聽伽（jia）利略的故事；愛好讀書，愛好科學；一直讀到萊比錫大學．1621年又到耶拿大學攻讀法律；1623年，再到萊頓大學鑽研數學和力學．他讀了三所大學，知識面很廣．因此，他能在軍旅中生活；又可在政界中立足；更能在科學界發言．他是1631年入伍，在軍隊中擔任軍械工程師，工作很出色．後來，投身政界，1646年當選為馬德堡市市長．無論在軍旅中，還是在市府內，都沒停止科學探索。
1654年，他聽到托里拆利的事兒，又聽說還有許多人不相信大氣壓；還聽到有少數人在嘲笑托里拆利；再聽說雙方爭論得很激烈，互不相讓，針鋒相對．因此，格里克雖在遠離德國的義大利，但很抱不平，義憤填膺．
他匆匆忙忙找來玻璃管子和水銀，重新做托里拆利這個實驗，斷定這個實驗是準確無誤的；他將一個密封完好的木桶中的空氣抽走，木桶就“砰！”的一聲被大氣“壓”碎了！有一天，他和助手做成兩個半球，直徑14英寸，即30多厘米，並請來一大隊人馬，在市郊做起“大型實驗”。
證明與測定
1 馬德堡半球實驗：（由馬德堡市長發起）
有力地證明了：①大氣壓的存在②大氣壓很大。
2 托里拆利實驗：在長約1m，一段封閉的玻璃管里灌滿水銀，用手指將管口堵住，然後倒插在水銀槽中。放開手指，管內水銀下降到一定程度時就不再下降，這時管內外水銀高度差約為760mm，把玻璃管傾斜，則水銀柱的長度變長，但水銀柱的高度，即玻璃管內外水銀面的高度差不變。測量結果表明這個高度是由當時的大氣壓的大小和水銀的密度所共同決定的，與玻璃管的粗細、形狀、長度(足夠長的玻璃管)無關。標準大氣壓(standardatmospheric pressure)的符號為1atm(非法定單位)，1atm*約為1.013×10的5次方Pa(在海平面的大氣壓)。
影響大氣壓強的因素
①溫度：溫度越高，空氣分子運動的越強烈，壓強越大.
②密度：密度越大，表示單位體積內空氣品質越大，壓強越大.
③海拔高度：海拔高度越高，空氣越稀薄，大氣壓強就越小。
pv=nRT克拉伯龍方程式也稱為理想氣體狀態方程通常用下式表示：pv=nRT……①
p表示壓強、V表示氣體體積、n表示物質的量、T表示絕對溫度、R表示氣體常數。所有氣體R值均相同。如果壓強、溫度和體積都採用國際單位（SI），R=8.314帕·米3/摩爾·K。如果壓強為大氣壓，體積為升，則R=0.0814大氣壓·升/摩爾·K。R 為常數
已知標準狀況下，1mol理想氣體的體積約為22.4L
把p=101325Pa,T=273.15K,n=1mol,V=22.4L代進去
得到R約為8314 帕·升/摩爾·K
玻爾茲曼常數的定義就是k=R/NA
因為n=m/M、ρ=m/v（n—物質的量，m—物質的質量，M—物質的摩爾質量，數值上等於物質的分子量，ρ—氣態物質的密度），所以克拉伯龍方程式也可寫成以下兩種形式：
pv=mRT/M……②和pM=ρRT……③
以A、B兩種氣體來進行討論。
1．在相同T、p、v時：
根據①式：nA=nB（即阿佛加德羅定律）
摩爾質量之比=分子量之比=密度之比=相對密度）。若mA=mB則MA=MB。
2．在相同T·p時：
體積之比=摩爾質量的反比；兩氣體的物質的量之比=摩爾質量的反比）
物質的量之比=氣體密度的反比；兩氣體的體積之比=氣體密度的反比）。
3．在相同T·v時：
摩爾質量的反比：兩氣體的壓強之比=氣體分子量的反比。
阿伏加德羅定律推論
一、阿伏加德羅定律推論
我們可以利用阿伏加德羅定律以及物質的量與分子數目、摩爾質量之間的關係得到以下有用的推論：
(1)同溫同壓時：①V1:V2=n1:n2=N1:N2 ②ρ1:ρ2=M1:M2 ③ 同質量時：V1:V2=M2:M1
(2)同溫同體積時：④ p1:p2=n1:n2=N1:N2 ⑤ 同質量時：p1:p2=M2:M1
(3)同溫同壓同體積時：⑥ ρ1:ρ2=M1:M2=m1:m2
具體的推導過程請大家自己推導一下，以幫助記憶。推理過程簡述如下：
(1)、同溫同壓下，體積相同的氣體就含有相同數目的分子，因此可知：在同溫同壓下，氣體體積與分子數目成正比，也就是與它們的物質的量成正比，即對任意氣體都有V=kn；因此有V1:V2=n1:n2=N1:N2，再根據n=m/M就有式②；若這時氣體質量再相同就有式③了。
(2)、從阿佛加德羅定律可知：溫度、體積、氣體分子數目都相同時，壓強也相同，亦即同溫同體積下氣體壓強與分子數目成正比。其餘推導同(1)。
(3)、同溫同壓同體積下，氣體的物質的量必同，根據n=m/M和ρ=m/V就有式⑥。當然這些結論不僅僅只適用於兩種氣體，還適用於多種氣體。
二、相對密度
在同溫同壓下，像在上面結論式②和式⑥中出現的密度比值稱為氣體的相對密度D=ρ1:ρ2=M1:M2。
注意：①D稱為氣體1相對於氣體2的相對密度，沒有單位。如氧氣對氫氣的密度為16。
②若同時體積也相同，則還等於質量之比，即D=m1:m2。
單位換算
單位
帕斯卡(Pa)
巴(bar)
工程大氣壓(at)
標準大氣壓(atm)
托(torr)
磅每平方英寸(psi)
換算
1 Pa = 1 N/平方m; = 10−5 bar ≈ 10.197×10−6 at ≈ 9.8692×10−6 atm ≈ 7.5006×10−3 Torr ≈ 145.04×10−6 psi
1 bar = 100 000 Pa = 106 dyn/cm² ≈ 1.0197 at ≈ 0.98692 atm ≈ 750.06 Torr ≈ 14.504 psi
1 at = 98 066.5 Pa = 0.980665 bar =1 kgf/cm² ≈ 0.96784 atm ≈ 735.56 Torr ≈ 14.223 psi
1 atm = 101 325 Pa = 1.01325 bar ≈ 1.0332 at =101 325 Pa = 760 Torr ≈ 14.696 psi
1 torr ≈ 133.322 Pa ≈ 1.3332×10−3 bar ≈ 1.3595×10−3 at ≈ 1.3158×10−3 atm = 1 mmHg ≈ 19.337×10−3 psi
1 psi ≈ 6894.76 Pa ≈ 68.948×10−3 bar ≈ 70.307×10−3 at ≈ 68.046×10−3 atm ≈ 51.715 Torr =1 lbf/in²
為方便記憶，可以簡化為如下規律：
1. 1atm=0.1MPa=100KPa=1公斤=1bar=10米水柱＝14.5PSI
2. 1KPa=0.01公斤=0.01bar=10mbar=7.5mmHg=0.3inHg=7.5torr=100mmH2O=4inH2O
大氣壓力、表壓力與絕對壓力的關係
(1)大氣壓力（atm）：大氣壓力是地球表面上空氣柱的重量所產生的壓力。用符號PB表示，大氣壓力值隨氣象情況、海拔高度和地理緯度等不同而改變。
(2)表壓力：測壓儀表所指示的壓力稱為表壓力，它是以大氣壓力為零起算的壓力。用符號PG表示．表壓力是通常工程中實用壓力。如kPaG、PSIG表示表壓力.
(3)絕對壓力：是指不附帶任何條件起算的全壓力。即液體、氣體和蒸汽所處空間的全部壓力。它等於大氣壓力和表壓力之和．用符號PA表示,如kPaA、PSIA表示絕對壓力.
PA＝PG十PB
說明
不少學科常常把壓強叫做壓力，同時把壓力叫做總壓力。這時的壓力不表示力，而是表示垂直作用於物體單位面積上的力。所以不再考慮力的矢量性和接觸面的矢量性，而將壓力作為一個標量來處理。
壓力與壓強
任何物體能承受的壓強有一定的限度，超過這個限度，物體就會損壞。物體由於外因或內因而形變時，在它內部任一截面的兩方即出現相互的作用力，單位截面上的這種作用力叫做壓力。
一般地說，對於固體，在外力的作用下，將會產生壓（或張）形變和切形變。因此，要確切地描述固體的這些形變，我們就必須知道作用在它的三個互相垂直的面上的力的三個分量的效果。這樣，對應於每一個分力Fx、Fy、Fz、以作用於Ax、Ay、Az三個互相垂直的面，應力F/A有九個不同的分量，因此嚴格地說應力是一個張量。
由於流體不能產生切變，不存在切應力。因此對於靜止流體，不管力是如何作用，只存在垂直於接觸面的力；又因為流體的各向同性，所以不管這些面如何取向，在同一點上，作用於單位面積上的力是相同的。由於理想流體的每一點上，F/A在各個方向是定值，所以應力F/A的方向性也就不存在了，有時稱這種應力為壓力，在中學物理中叫做壓強。壓強是一個標量。壓強（壓力）的這一定義的套用，一般總是被限制在有關流體的問題中。
垂直作用於物體的單位面積上的壓力。若用P表示壓強，單位為帕斯卡（1帕斯卡=1牛頓/平方米）(1Pa=1N/m2)
非矢量性
既然壓強是脅強的一種，這已經說明壓強不是矢量了。對此，還可以進一步說明如下：取包含物體內任一點O的面元ds，任意力F或dF作用在該面元上，與面元的法線方向夾角，如圖（2）。力F對面元ds產生的壓強是F在ds的法冋分量與ds的比值Fy/ds，F在與ds平行方向的分量Fx對面元ds說來是切強（切脅強）。再取包含O點在內的與ds正交的面元ds'，不難看出，這時FY/ds’是切強，Fx/ds’是壓強。這說明：同一力作用在同一點上，由於所取面元的方位不同，產生的效果也不一樣，就是說壓強與所取面元的方向有關。於是，在研究壓強時不僅要考慮力的方向，還應該確定面的方向；通常取面元的正法線方向為面的方向，這樣，面也是矢量。
由公式F=pS可知：F是矢量，S（ds）也是矢量，且F的方向與S的方向總是一致的，p必然不能是矢量。因為如果P也是矢量，則P與S的乘壓強不是矢量，其實也不是標量。因為決定脅強的力和面積都是矢量，每個矢量都有三個分量。在彈性力學中，脅強是由力和面積決定的量有九個分量的量，稱為張量。而壓強則是張量中最簡單的一個量，關於張量的概念和運算，已超出中學物理的範圍，我們在此從略。
液壓
液體容器底、內壁、內部的壓強稱為液體壓強，簡稱液壓。
（一）液體壓強原理（帕斯卡定律）的產生帕斯卡發現了液體傳遞壓強的基本規律，這就是著名的帕斯卡定律．所有的液壓機械都是根據帕斯卡定律設計的，所以帕斯卡被稱為“液壓機之父”。
在幾百年前，帕斯卡注意到一些生活現象，如沒有灌水的水龍帶是扁的．水龍帶接到自來水龍頭上，灌進水，就變成圓柱形了．如果水龍帶上有幾個眼，就會有水從小眼裡噴出來，噴射的方向是向四面八方的。水是往前流的，為什麼能把水龍帶撐圓？
通過觀察，帕斯卡設計了“帕斯卡球”實驗，帕斯卡球是一個壁上有許多小孔的空心球，球上連線一個圓筒，筒里有可以移動的活塞．把水灌進球和筒里，向里壓活塞，水便從各個小孔里噴射出來了，成了一支“多孔水槍”。
帕斯卡球的實驗證明，液體能夠把它所受到的壓強向各個方向傳遞．通過觀察發現每個孔噴出去水的距離差不多，這說明，每個孔所受到的壓強都相同。
帕斯卡通過“帕斯卡球”實驗，得出著名的帕斯卡定律：加在密閉液體任一部分的壓強，必然按其原來的大小，由液體向各個方向傳遞。
（二）液體壓強（帕斯卡定律）的原理
我們知道，物體受到力的作用產生壓力，而只要某物體對另一物體表面有壓力，就存在壓強，同理，水由於受到重力作用對容器底部有壓力，因此水對容器底部存在壓強。液體具有流動性，對容器壁有壓力，因此液體對容器壁也存在壓強。
在國中階段，液體壓強原理可表述為：“液體內部向各個方向都有壓強，壓強隨液體深度的增加而增大，同種液體在同一深度的各處，各個方向的壓強大小相等；不同的液體，在同一深度產生的壓強大小與液體的密度有關，密度越大，液體的壓強越大。”
（三）液體內部壓強：
一、同種液體
1．向各個方向都有壓強
2．同一深度處，壓強一致
3．深度越深，壓強越大
二、不同液體
同一深度，密度越大，壓強越大
公式：p=ρgh 式中g=9.8N/kg 或g=10N/kg，h的單位是m，ρ的單位是kg/m^3，壓強p的單位是Pa。
公式推導：
壓強公式均可由基礎公式：p=F/S推導
p=F/S=G/S=mg/S=ρVg/S=ρShg/S=ρhg=ρghF=ρ液gh，h是深度。
深度是指點到自由液面的距離，液體的壓強只與深度和液體的密度有關，與液體的質量無關。
（四）什麼是液體壓強
1．液體壓強產生的原因是由於液體受重力的作用。若液體在失重的情況下，將無壓強可言。
2．由於液體具有流動性，它所產生的壓強具有如下幾個特點
(1)液體除了對容器底部產生壓強外，還對“限制”它流動的側壁產生壓強。固體則只對其支承面產生壓強，方向總是與支承面垂直。
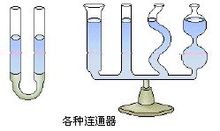連通器內液體不流動時各容器中液面高度相同(2)在液體內部向各個方向都有壓強，在同一深度向各個方向的壓強都相等。
(3)計算液體壓強的公式是p=ρgh。可見，液體壓強的大小隻取決於液體的種類（即密度ρ）和深度h，而和液體的質量、體積沒有直接的關係。
(4)密閉容器內的液體能把它受到的壓強按原來的大小向各個方向傳遞。
3．容器底部受到液體的壓力跟液體的重力不一定相等。容器底部受到液體的壓力F=pS=ρghS，其中“h、S”底面積為S，高度為h的液柱的體積，“ρghS”是這一液柱的重力。因為液體有可能傾斜放置。所以，容器底部受到的壓力其大小可能等於，也可能大於或小於液體本身的重力。
（五）液U形管壓強計體壓強的測量
液體壓強的測量儀器叫“U形管壓強計”，利用液體壓強公式p=ρhg，h為兩液面的高度差，計算液面差產生的壓強就等於液體內部壓強。
公式：F1/S1=F2/S2
非直立柱體時液體對容器底部的壓強，可用p=ρgh計算，不能用p=F/S計算；非直立柱體時液體對容器底部的壓力，可用F=pS=ρghS計算。因為同學對這個問題疑問較多，對p=F/S和p=ρgh兩個公式簡單說明如下：由P=F/S是可以推導出液體壓強公式 p=ρgh，但這是在液體容器為規則均勻的柱體容器的前提下推導出來的，所以公式 p=F/S的使用條件僅適用於這種柱體容器（這一點與固體不同，固體間的壓強總是可以用p=F/S來計算）。但 p=ρgh這個公式根據液體本身的特性（易流性，連通器原理、帕斯卡定律等）可以推廣到任意形狀的容器，只要是連通的密度均勻的液體都可以用。其實液體內部壓強公式的推導完全可以不用公式p=F/S來推導，而是用更加普遍、更加一般的方法——質量力的勢函式的積分來推導，只是這已超出中學的教學大綱了。由於液體的易流性和不可拉性，靜止的液體內部沒有拉應力和切應力，只能有壓應力（即壓強），在靜止的液體內部任意取出微小一個六面體，這個六面體在六個面的壓力和本身的重力共同作用下處於平衡狀態，構想這個六面體無限縮小時，其重力可以忽略不計，就得出作用在同一點上的各個方向的壓強相等，即壓強僅僅與位置坐標有關，而與方位無關。即 P=f(x,y,z)。再構想坐標x-O-y處在水平面上，z為豎直向下的坐標。液體的壓強是由液體的質量力引起的，當液體對地球來說是靜止時，就是由重力引起的，液體質量m=1的液體單位質量力在各坐標的分量為X=0、Y=0、Z=g，液體內部的壓強與質量力的微分關係為dp=ρ（XdxYdy+Zdz）=ρ（0*dx+0*dy+gdz）=ρgdz （從本方程看出在同一水平面上沒有壓強差，水平面是等壓面，即前後左右壓強都相等，壓強僅在重力方向上有變化）。從水面z=0到水深z=h積分上式得 p=ρgh。
同一深度，密度越大，壓強越大。
液體內部壓強：p=ρgh（式中ρ表示液體密度，g表示重力加速度，h表示液體深度）
如果題中沒有明確提出g等於幾，套用g=9.8N/kg，再就是題後邊基本上都有括弧，括弧的內容就是g和ρ的值。
公式推導：壓強公式均可由基礎公式：p=F/S推導
p液=F/S=G/S=mg/S=ρ液Vg/S=ρ液Shg/S=ρ液hg=ρ液gh。
由於液體內部同一深度處向各個方向的壓強都相等，所以我們只要算出液體豎直向下的壓強，也就同時知道了在這一深度處液體向各個方向的壓強。這個公式定量地給出了液體內部壓強地規律。
深度是指點到自由液面的距離，液體的壓強與深度和液體的密度有關，與液體的質量無關。
液體壓強產生原因：受重力、且有流動性。
影響液體壓強的因素：深度，液體的密度（與容器的形狀，液體的質量體積無關）
液體壓強的測量的儀器叫U形管壓強計，利用液體壓強公式p=phg，h為兩液面的高度差，計算液面差產生的壓強就等於液體內部壓強。
套用
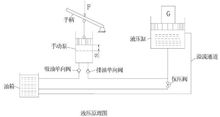壓強液壓千斤頂，用吸管吸飲料，吸盤貼在光滑的牆壁上不脫落，用針管吸水，拔火罐等。活塞式抽水機，根據大氣壓強可算出活塞式抽水機最高能將水抽上10米。
