代數基本定理
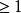復係數多項式因式分解定理每個次數的復係數多項式在複數域中有一個根.
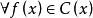復係數多項式因式分解定理
復係數多項式因式分解定理
復係數多項式因式分解定理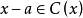
復係數多項式因式分解定理
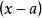復係數多項式因式分解定理推論1： ,若 ,則存在 ,使得 |
即代數基本定理可以等價地敘述為：每個次數的復係數多項式在複數域上一定有一個一次因式。
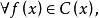復係數多項式因式分解定理
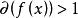復係數多項式因式分解定理 復係數多項式因式分解定理推論2：複數域上不可約多項式只有一次多項式。即 若 ，則 可約。
復係數多項式因式分解定理及推論
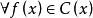復係數多項式因式分解定理
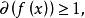復係數多項式因式分解定理 復係數多項式因式分解定理,若 則 在複數域上可唯一分解成一次因式的乘積。
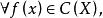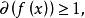復係數多項式因式分解定理 復係數多項式因式分解定理 復係數多項式因式分解定理推論1： 若 則 在複數域上具有標準分解式。
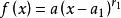復係數多項式因式分解定理
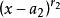復係數多項式因式分解定理
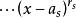復係數多項式因式分解定理
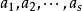復係數多項式因式分解定理
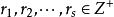復係數多項式因式分解定理其中 是不同的複數，
推論2：每個n次復係數多項式恰好有n個根（重根按重數計算）。
套用舉例
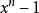復係數多項式因式分解定理求 在複數域上的標準分解式
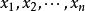復係數多項式因式分解定理證：由定理推論2得，在複數域上原式有n個根
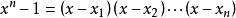復係數多項式因式分解定理因此，,其中
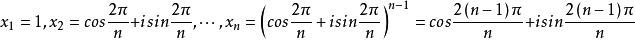復係數多項式因式分解定理