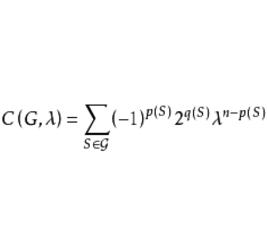基本介紹
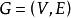 圈多項式
圈多項式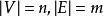 圈多項式
圈多項式 圈多項式
圈多項式考察有向(無向)簡單圖,其中,必要時也可以考慮有自環(loop)的有向圖,今後分別以V(S)及E(S)表示子圖S的頂點集及邊集;記號表示子圖的並運算。
相關定義
 圈多項式
圈多項式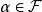 圈多項式
圈多項式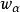 圈多項式
圈多項式 圈多項式
圈多項式定義1取定圖G的一個子圖族;對其中每一個子圖,賦以某一整環R中之元,作為它的度量,這樣一個具有度量的子圖族便稱為“ 覆蓋單元集”;其中每一個子圖α稱為“ (覆蓋)單元”。
 圈多項式
圈多項式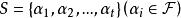 圈多項式
圈多項式定義2對於不含全不連通子圖的覆蓋單元集而言,圖G的一個“ 邊覆蓋”,是指由若干個無公共邊的單元所組成的集合,使得
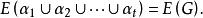 圈多項式
圈多項式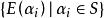 圈多項式
圈多項式換言之,構成邊集E(G)的一個劃分。
 圈多項式
圈多項式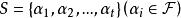 圈多項式
圈多項式定義2’對給定的覆蓋單元集而言,圖G的一個“ 點覆蓋”,是指由若干個無公共頂點的單元所組成的集合,使得
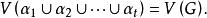 圈多項式
圈多項式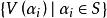 圈多項式
圈多項式換言之,構成頂點集V(G)的一個劃分。
邊(點)覆蓋多項式
 圈多項式
圈多項式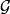 圈多項式
圈多項式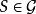 圈多項式
圈多項式定義3對給定的覆蓋單元集,設圖G所有邊(點)覆蓋所構成的集族為,對每一覆蓋,賦以一個單項式
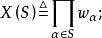 圈多項式
圈多項式進而對圖G賦以一個多項式
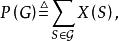 圈多項式
圈多項式 圈多項式
圈多項式這個P(G)便稱為圖G在之下的“ 邊(點)覆蓋多項式”。
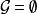 圈多項式
圈多項式 圈多項式
圈多項式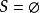 圈多項式
圈多項式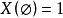 圈多項式
圈多項式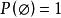 圈多項式
圈多項式下文始終採取“空和為零,空積為1“的習慣約定,因此,當時,P(G)=0,當G=(空圖)時,只有一個覆蓋;而,所以。其次,在邊覆蓋多項式的情況,增減一些孤立頂點時邊覆蓋不變,因而多項式亦不變;故此時不妨假定圖G並無孤立頂點 。
圈多項式的定義
 圈多項式
圈多項式 圈多項式
圈多項式在無向圖的情況,設由G中所有的K(一點生成子圖)、K(一邊生成子圖)及初級圈(點數≥3)所構成,R為實數域上的多項式環,由此產生出的點覆蓋多項式通常稱為“ 圈多項式”,特別當單元K的度量為(未定元),K的度量為-1,其它初級圈的度量為-2時,點覆蓋多項式
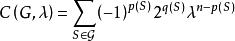 圈多項式
圈多項式就是熟知的特徵多項式,其中p(S)為S中有邊的單元數,q(S)為S中的圈數。
相關概念
子圖多項式
 圈多項式
圈多項式 圈多項式
圈多項式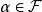 圈多項式
圈多項式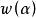 圈多項式
圈多項式當G為無向圖,由G的一切連通子圖所構成時,圖G在之下的點覆蓋多項式稱為“ 子圖多項式”,而當單元的度量不同時,可得一些特殊的多項式,例如:
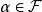 圈多項式
圈多項式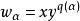 圈多項式
圈多項式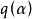 圈多項式
圈多項式(1°) 對每一單元,賦以度量,其中為連通子圖α的圈秩,那么圖G在這種覆蓋意義下的多項式
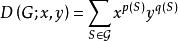 圈多項式
圈多項式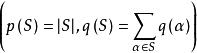 圈多項式
圈多項式就是 雙色多項式,其中p(S)及q(S)分別表示由S的單元的並所構成的支撐子圖的分圖數及圈秩。
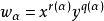 圈多項式
圈多項式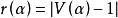 圈多項式
圈多項式(2°) 若令,其中為連通子圖α的秩,則
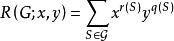 圈多項式
圈多項式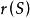 圈多項式
圈多項式就是 秩多項式,其中,表示由S所成的支撐子圖的秩。
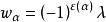 圈多項式
圈多項式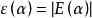 圈多項式
圈多項式(3°) 若令,其中為連通子圖α的邊數,則
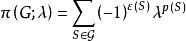 圈多項式
圈多項式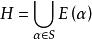 圈多項式
圈多項式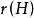 圈多項式
圈多項式就是 色多項式,事實上,記,並以表示H的生成子圖的秩,則上式可改寫為
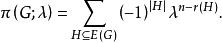 圈多項式
圈多項式這就是 色多項式的展開式(極易由容斥原理推出)。
匹配多項式
 圈多項式
圈多項式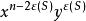 圈多項式
圈多項式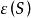 圈多項式
圈多項式設由G中所有子圖K及K所構成,它們的度量分別為x及y,由這種單元組成的點覆蓋S就是圖G的“ 匹配”(matching);它對應的單項式為,其中為S中單元K的數目(邊數),於是
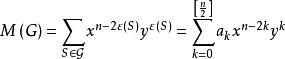 圈多項式
圈多項式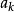 圈多項式
圈多項式就是圖G的 匹配多項式,其中為k邊匹配的數目 。
相關定理
 圈多項式
圈多項式設圖G= (V,E)在單元集之下的邊(點)覆蓋多項式為P(G),下面將給出這兩類多項式的一般消去定理。
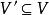 圈多項式
圈多項式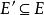 圈多項式
圈多項式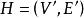 圈多項式
圈多項式定義4對任意的頂點子集及邊子集,二元組稱為G的“偽子圖”。
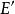 圈多項式
圈多項式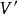 圈多項式
圈多項式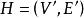 圈多項式
圈多項式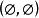 圈多項式
圈多項式 圈多項式
圈多項式當中每條邊所關聯的頂點均屬於時,就是通常意義的子圖,將簡記為。
定義5給定G的一個偽子圖H,圖G關於H的部分邊(點) 覆蓋S,是指由若干個無公共邊(點)的單元所組成的集合,這些單元的並包含了H的全部頂點和邊,且每個單元都至少含有H的一個頂點或一條邊。
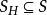 圈多項式
圈多項式對於圖G的一個邊(點)覆蓋S 而言,如果S覆蓋著H的點和邊,則將S 中含有H的頂點或邊的單元取出來,這樣構成的子集S一定是關於H的部分覆蓋,即有,但反過來說,一個部分覆蓋卻不一定能成為某個覆蓋的子集(它未必能添上一些單元後構成G的覆蓋)。
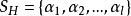 圈多項式
圈多項式定義6對部分邊(點)覆蓋而言,其相應的單項式定義為
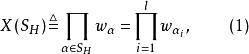 圈多項式
圈多項式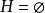 圈多項式
圈多項式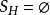 圈多項式
圈多項式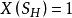 圈多項式
圈多項式特別當,因而時,。
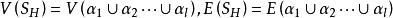 圈多項式
圈多項式此外,我們記。
現在,分兩種情況討論。
邊覆蓋多項式的消去定理
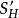 圈多項式
圈多項式定義7一個關於H的部分邊覆蓋S稱為極大的,如果不存在以它為真子集的另一個關於H的部分邊覆蓋。
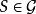 圈多項式
圈多項式命題 對任一個邊覆蓋,由其中所有含有H的頂點或邊的單元所構成的部分邊覆蓋S一定是極大的。
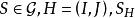 圈多項式
圈多項式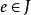 圈多項式
圈多項式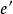 圈多項式
圈多項式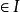 圈多項式
圈多項式證明:設是按上述方式導出的部分邊覆蓋,那么H中的邊()及H中的頂點所關聯的邊(的端點)均被S的單元所覆蓋;而任一單元均非孤立點,所以不存在這樣的單元,它與S的單元無公共邊而又包含H的頂點或邊,故S為極大的。
 圈多項式
圈多項式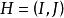 圈多項式
圈多項式定理1設圖G在單元集之下的邊覆蓋多項式為P(G),並設為G的一個偽子圖,則
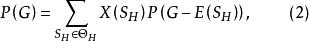 圈多項式
圈多項式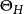 圈多項式
圈多項式其中為G關於H的一切極大的部分邊覆蓋的集合。
點覆蓋多項式的消去定理
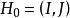 圈多項式
圈多項式取定圖G的一個偽子圖,考察由它除去一些邊所成的偽子圖H的集合
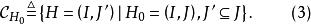 圈多項式
圈多項式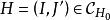 圈多項式
圈多項式對於每一個,又考察部分點覆蓋的集合
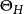 圈多項式
圈多項式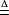 圈多項式
圈多項式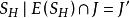 圈多項式
圈多項式{部分點覆蓋}. (4)
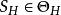 圈多項式
圈多項式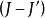 圈多項式
圈多項式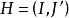 圈多項式
圈多項式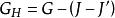 圈多項式
圈多項式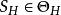 圈多項式
圈多項式就是G關於H的部分點覆蓋,它的單元包含J' 的邊,而不包含的邊。為更明顯起見,對於,我們令。那么,就是圖G關於H的部分點覆蓋。
 圈多項式
圈多項式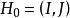 圈多項式
圈多項式定理2 設圖G在單元集之下的點覆蓋多項式為P(G),並設為G的一個偽子圖,則
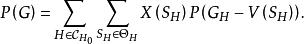 圈多項式
圈多項式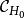 圈多項式
圈多項式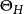 圈多項式
圈多項式其中集合及分別由(3)(4)式所定義 。