基本知識
相關知識
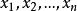 多元多項式
多元多項式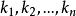 多元多項式
多元多項式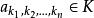 多元多項式
多元多項式設K是一個數域, 是幾個文字(也可稱為變數), 是非負整數, ,稱
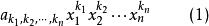 多元多項式
多元多項式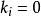 多元多項式
多元多項式 多元多項式
多元多項式 多元多項式
多元多項式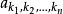 多元多項式
多元多項式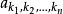 多元多項式
多元多項式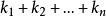 多元多項式
多元多項式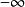 多元多項式
多元多項式為一個 單項式(monomial)。某個指數 表示變數 不出現,當所有的指數全部等於0時,相應的單項式就是常數項 , 稱為此單項式的 係數,當 ≠0時, 稱為此單項式的 次數,係數為0的單項式稱為 零單項式,簡記為0,零單項式的次數規定為 ,為了表示方便,常常把單項式(1)中各個字母的方冪看成一個n維向量
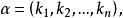 多元多項式
多元多項式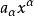 多元多項式
多元多項式 多元多項式
多元多項式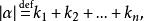 多元多項式
多元多項式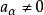 多元多項式
多元多項式稱為這個單項式的 指數向量。並把單項式(1)簡記為 ,又把向量 的分量之和表為 ,於是有(假設 )
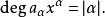 多元多項式
多元多項式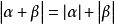 多元多項式
多元多項式顯然指數向量的分量都是非負整數,因此有 兩個單項式:
 多元多項式
多元多項式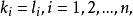 多元多項式
多元多項式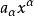 多元多項式
多元多項式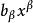 多元多項式
多元多項式 多元多項式
多元多項式如果滿足 就被稱為 同類項,也就是說, 與 是同類項若且唯若它們的指數向量相等,即 。
n元多項式的定義
有限多個單項式之和(假設其中不含同類項)
 多元多項式
多元多項式 多元多項式
多元多項式 多元多項式
多元多項式 多元多項式
多元多項式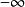 多元多項式
多元多項式稱為 n元多項式,簡稱 多項式,n 元多項式 中非零單項式的最高次數稱為多項式 的 次數,記為 。只含零單項式的多項式稱為 零多項式,記為0,零多項式的次數規定為 ,例如若
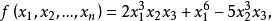 多元多項式
多元多項式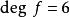 多元多項式
多元多項式則 。
 多元多項式
多元多項式有很多時候需要把多元多項式看成其中某一個變數,例如 的一元多項式
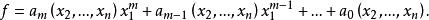 多元多項式
多元多項式 多元多項式
多元多項式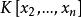 多元多項式
多元多項式 多元多項式
多元多項式 多元多項式
多元多項式 多元多項式
多元多項式 多元多項式
多元多項式 多元多項式
多元多項式這裡的係數 都是多項式環 中的元素,我們把 作為某個變數 的一元多項式的次數稱為 關於 的次數,記為 。
和一元多項式一樣,對於n元多項式也可同樣地定義相等、相加、相減和相乘,例如當兩個單項式是同類項時,可以通過係數相加而合併成一項:
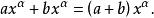 多元多項式
多元多項式兩個單項式相乘則是把指數向量相加,再把係數相乘:
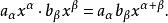 多元多項式
多元多項式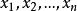 多元多項式
多元多項式n元多項式的加法和乘法具有與一元多項式相同的性質,因此把數域K上所有以 為變數的n元多項式的集合記為
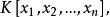 多元多項式
多元多項式並稱為數域K上的 n元多項式環。
多項式的排序問題
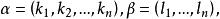 多元多項式
多元多項式 多元多項式
多元多項式現在我們要研究 單項式的排序問題,對於一元多項式,按各個項的次數來排列是最自然的,但是對於多元多項式,有相同次數的項不止一個,單按次數排列具有不確定性,所以有必要採用 字典排列法。為此首先在指數向量的集合內定義一個序:對於 ,如果存在 使得
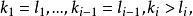 多元多項式
多元多項式 多元多項式
多元多項式 多元多項式
多元多項式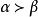 多元多項式
多元多項式則稱 優於 ,記為 ,例如
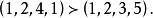 多元多項式
多元多項式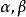 多元多項式
多元多項式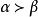 多元多項式
多元多項式 多元多項式
多元多項式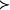 多元多項式
多元多項式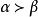 多元多項式
多元多項式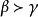 多元多項式
多元多項式 多元多項式
多元多項式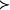 多元多項式
多元多項式從這個定義立即可以看出,對於任意兩個不相等的指數向量 ,不是 就是 ,兩者必居其一。而且關係“ ”還具有傳遞性,即從 與 可以得出 ,這說明“ ”確實是指數向量集合的一個序,利用指數向量的序就可以定義單項式的序,即
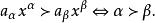 多元多項式
多元多項式我們把這個序(包括指數向量的序以及單項式的序)稱為 字典序(lexicographicorder)。這樣就可以把多項式中的項按字典序排列,當n=1時這種排列法就是 降冪排列法,多項式中按字典排列法次序最前的非零項稱為此 多項式的首項。
相關性質
字 典排列法的首項有以下性質。
定理1
兩個非零多項式的乘積的首項等於這兩個多項式的首項的乘積。
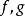 多元多項式
多元多項式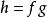 多元多項式
多元多項式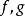 多元多項式
多元多項式證明:設這兩個多項式是 ,它們的乘積是 .設 的首項分別為
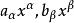 多元多項式
多元多項式它們的乘積等於
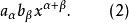 多元多項式
多元多項式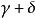 多元多項式
多元多項式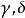 多元多項式
多元多項式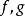 多元多項式
多元多項式乘積多項式h中的任意單項式的指數向量具有 的形式,其中, 分別是 中的單項式的指數向量,因此有
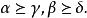 多元多項式
多元多項式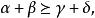 多元多項式
多元多項式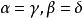 多元多項式
多元多項式 多元多項式
多元多項式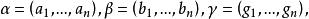 多元多項式
多元多項式我們要證 ,並且等號成立若且唯若 。首先設 若 ,則一定存在i≤n使得
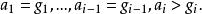 多元多項式
多元多項式於是
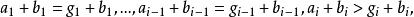 多元多項式
多元多項式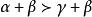 多元多項式
多元多項式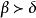 多元多項式
多元多項式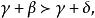 多元多項式
多元多項式即 。同理當 時有 因此
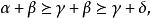 多元多項式
多元多項式 多元多項式
多元多項式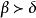 多元多項式
多元多項式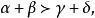 多元多項式
多元多項式而且只要 或 有一個成立,就有 這說明(2)式確是h的首項而且h中沒有同類項會和它相消。
推論2
兩個非零多項式的乘積仍是非零多項式。