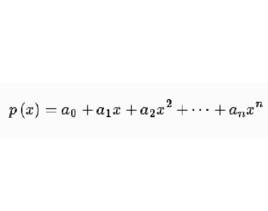定義
我們把形如
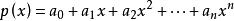 整係數多項式
整係數多項式 整係數多項式
整係數多項式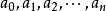 整係數多項式
整係數多項式 整係數多項式
整係數多項式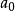 整係數多項式
整係數多項式 整係數多項式
整係數多項式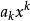 整係數多項式
整係數多項式 整係數多項式
整係數多項式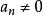 整係數多項式
整係數多項式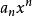 整係數多項式
整係數多項式 整係數多項式
整係數多項式 整係數多項式
整係數多項式 整係數多項式
整係數多項式 整係數多項式
整係數多項式 整係數多項式
整係數多項式 整係數多項式
整係數多項式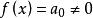 整係數多項式
整係數多項式 整係數多項式
整係數多項式的表達式叫做x的多項式,記為 ,其中n是正整數,x是一個符號(或文字), 都是常數,叫做 的 係數, 還叫做 的 常數項。 叫做 一個項,k叫做這一項的 次數。當 時, 叫做 的 首 項, 叫做 首項係數,n叫做 的次數,記為次 .如果 的係數全為零,則把 叫做 零多項式,記為0。我們認為零多項式沒有次數,若 ,則說 是零次多項式。
 整係數多項式
整係數多項式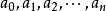 整係數多項式
整係數多項式 整係數多項式
整係數多項式 整係數多項式
整係數多項式 整係數多項式
整係數多項式如果多項 的係數 都是整數,我們把 叫做 整係數多項式,如果 的係數都是有理數,就把 叫做 有理係數多項式。同樣地,可以定義 實係數 多項式和 復係數多項式。
相關性質
定理1
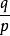 整係數多項式
整係數多項式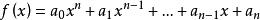 整係數多項式
整係數多項式(整係數多項式有理根的性質) 若既約分數 為整係數多項式 的根,則:
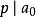 整係數多項式
整係數多項式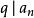 整係數多項式
整係數多項式(1) 且 ;
 整係數多項式
整係數多項式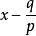 整係數多項式
整係數多項式(2) 除以 所得的商的各項係數必為p的倍數。
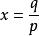 整係數多項式
整係數多項式 整係數多項式
整係數多項式證明:因為 為 的根。
所以,由因式定理,有
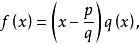 整係數多項式
整係數多項式其中
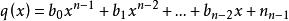 整係數多項式
整係數多項式為有係數多項式。由此可得
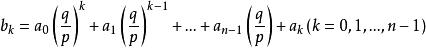 整係數多項式
整係數多項式可化為
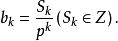 整係數多項式
整係數多項式由根的意義,有
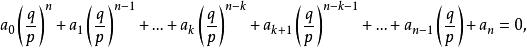 整係數多項式
整係數多項式可化為
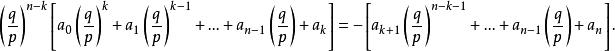 整係數多項式
整係數多項式故得
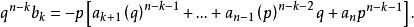 整係數多項式
整係數多項式①
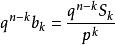 整係數多項式
整係數多項式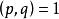 整係數多項式
整係數多項式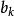 整係數多項式
整係數多項式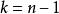 整係數多項式
整係數多項式可知 為整數,但 ,故 為整數,又 時,式①變為
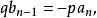 整係數多項式
整係數多項式由此得
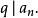 整係數多項式
整係數多項式推論1
最高次項係數為1的整係數多項式的有理根必為整數。
推論2
 整係數多項式
整係數多項式 整係數多項式
整係數多項式 整係數多項式
整係數多項式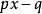 整係數多項式
整係數多項式若既約分數 為整係數多項式 的根,則除以 所得的商為整係數多項式。
定理2
 整係數多項式
整係數多項式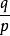 整係數多項式
整係數多項式 整係數多項式
整係數多項式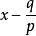 整係數多項式
整係數多項式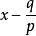 整係數多項式
整係數多項式 整係數多項式
整係數多項式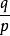 整係數多項式
整係數多項式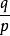 整係數多項式
整係數多項式求整係數多項式 的有理根的主要依據,其方法是:首先按定理1的結論(1)或其他有關條件找出有理根的一切可能根 ,然後採用綜合除法將 除以 ,根據因式定理,若且唯若 整除 時, 為有理根,除的過程中,如發現商的係數非p的倍數,則根據定理1的結論(2), 非有理根,可不必再除下去。
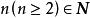 整係數多項式
整係數多項式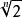 整係數多項式
整係數多項式例1設,求證:為無理數。
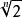 整係數多項式
整係數多項式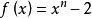 整係數多項式
整係數多項式證明:是整係數多項式的一根,
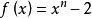 整係數多項式
整係數多項式可能的有理根為±1,±2,但
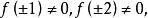 整係數多項式
整係數多項式 整係數多項式
整係數多項式所以無有理數根。
定理3
 整係數多項式
整係數多項式 整係數多項式
整係數多項式 整係數多項式
整係數多項式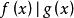 整係數多項式
整係數多項式設 為有理係數多項式, 與 有公共根a,則。
 整係數多項式
整係數多項式 整係數多項式
整係數多項式 整係數多項式
整係數多項式 整係數多項式
整係數多項式定理3的意義是,若有理係數不可約多項式有一根為另一有理係數多項式 的根,則 的全部根均為 的根。
推論3
 整係數多項式
整係數多項式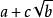 整係數多項式
整係數多項式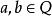 整係數多項式
整係數多項式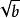 整係數多項式
整係數多項式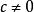 整係數多項式
整係數多項式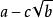 整係數多項式
整係數多項式如果有理係數多項式 有無理根 ( , 為無理數, ),則必有無理根。
推論4
 整係數多項式
整係數多項式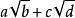 整係數多項式
整係數多項式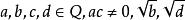 整係數多項式
整係數多項式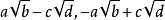 整係數多項式
整係數多項式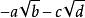 整係數多項式
整係數多項式如果有理係數多項式 有無理根 ( 為無理數且非同類根式),則必有無理根 及。