定義1
設
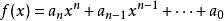有理係數多項式
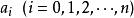有理係數多項式
有理係數多項式其中，每個係數屬於有理數，則稱為 有理係數多項式 。
有理係數多項式 有理係數多項式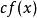
有理係數多項式 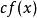有理係數多項式選取恰當的整數乘，總可以使是一整係數多項式。如果的各項係數有公因子，就可以提出來，得到
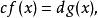有理係數多項式也就是
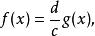有理係數多項式
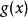有理係數多項式
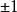有理係數多項式其中是整係數多項式，且各項係數沒有異於的公因子。
例如
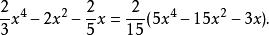有理係數多項式
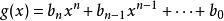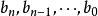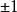有理係數多項式
有理係數多項式 有理係數多項式 有理係數多項式
有理係數多項式
有理係數多項式如果一個非零的整係數多項式的係數沒有異於的公因子，也就是說，它們是互素的，它就稱為一個 本原多項式。上面的分析表明，任何一個非零的有理係數多項式都可以表示成一個有理數與一個本原多項式的乘積，即
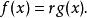有理係數多項式可以證明，這種表示方法除了差一個正負號是惟一的。亦即，如果
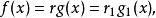有理係數多項式
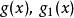有理係數多項式其中都是本原多項式，那么必有
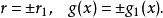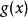有理係數多項式 有理係數多項式 有理係數多項式 有理係數多項式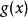 有理係數多項式因為與只差一個常數倍，所以的因式分解問題，可以歸結為本原多項式的因式分解問題。並且，一個本原多項式能否分解成兩個次數較低的有理係數多項式的乘積與它能否分解成兩個次數較低的整係數多項式的乘積的問題是一致的。
在有理係數多項式的因為分解問題中，我們有如下幾個定理 ：
定理1（高斯（Guass）引理）
兩個本原多項式的乘積還是本原多項式。
定理2
如果一個非零的整係數多項式能夠分解成兩個次數較低的有理係數多項式的乘積，那么它一定能分解成兩個次數較低的整係數多項式的乘積。
推論1
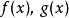有理係數多項式 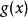有理係數多項式
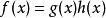有理係數多項式
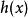有理係數多項式 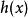有理係數多項式設是整係數多項式，且是本原的。如果，其中是有理係數多項式，那么一定是整係數的。
這個推論提供了一個求整係數多項式的全部有理根的方法。
定理3
設
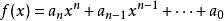有理係數多項式
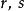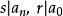有理係數多項式
有理係數多項式
有理係數多項式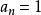 有理係數多項式
有理係數多項式 有理係數多項式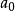
有理係數多項式是一個整係數多項式，而是它的一個有理根，其中互素，那么必有。特別地，如果的首項係數，那么的有理根都是整根，而且是的因子。
例1
求方程
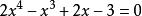有理係數多項式的有理根。
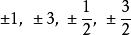有理係數多項式
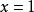有理係數多項式這個方程的有理根只可能是。用剩餘除法可以得出，除去1以外全不是它的根，因之這個方程的有理根只有。
例2
證明
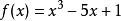有理係數多項式在有理數域上不可約。
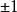有理係數多項式 有理係數多項式 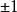有理係數多項式 有理係數多項式 有理係數多項式如果可約，那么它至少有一個一次因子，也就是有一個有理根。但是的有理根只可能是。直接驗算可知全不是根，因而在有理數域上不可約。
定理4（艾森斯坦（Eisenstein）判別法）
設
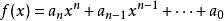有理係數多項式
有理係數多項式是一個整係數多項式。如果有一個素數，使得
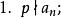有理係數多項式
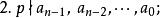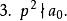有理係數多項式
有理係數多項式 有理係數多項式那么在有理數域上不可約的。
有理係數多項式根據定理4，可知對於任意的，多項式
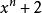有理係數多項式在有理數域上是不可約的。由此可見，在有理數域上，存在任意次數的不可約多項式。
