定義
均值定理：對於任意兩個正實數 a、 b，都有
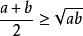均值定理若且唯若a=b時，等號成立。
注：運用均值不等式求最值條件
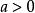均值定理
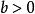均值定理① ， ；
② a和 b的乘積 ab是一個定值（正數）；
③等號成立條件。
相關重要不等式：
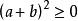均值定理① ；
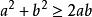均值定理② ；
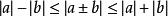均值定理③ 。
幾何含義
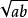均值定理
均值定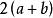理
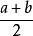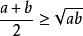均值定理 均值定理一個矩形的長為a，寬為b，畫兩個正方形，要求第一個正方形的面積與矩形的面積相同，第二個正方形的周長與矩形的周長相同，如圖1所示。第一個正方形的面積為ab，則其邊長為 ；第二個正方形的周長為 ，邊長為 。可以看出第一個正方形面積不大於第二個正方形，即邊長關係 。
圖1 均值定理幾何含義推廣
均值不等式
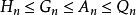均值定理均值定理可進行推廣，得到更為通用的均值不等式： 。即調和平均數不超過幾何平均數，幾何平均數不超過算術平均數，算術平均數不超過平方平均數，簡記為“調幾算方”。
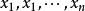均值定理其中：對於任意非負實數 ，有
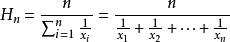均值定理，即調和平均數；
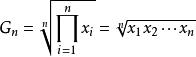均值定理，即幾何平均數；
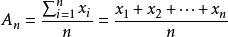均值定理，即為算術平均數；
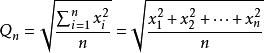均值定理，即為平方平均數。
例題
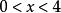均值定理
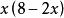均值定理（1）當 時，求 的最大值。
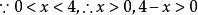均值定理解：
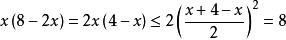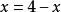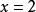均值定理
均值定理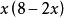
均值定理
均值定理若且唯若 ，即 時， 取最大值8。
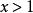均值定理
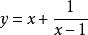均值定理（2）當 時，求函式 的最小值。
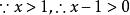均值定理解：
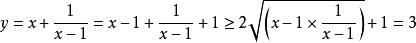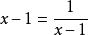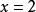均值定理
均值定理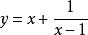 均值定理
均值定理若且唯若，即時，取最小值3。
