樣本
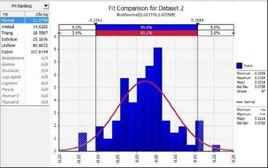
樣本(sample),是指從總體中抽出的一部分個體。樣本中所包含個體數目稱樣本容量或含量,用符號N或n表示。
總體(population)是指客觀存在的,並在同一性質的基礎上結合起來的許多個別單位的整體,即具有某一特性的一類事物的全體,又叫母體或全域。簡單地說,總體也就是我們所研究的性質相同個體的總和。
樣本是受審查客體的反映形象或其自身的一部分。按一定方式從總體中抽取的若干個體,用於提供總體的信息及由此對總體作統計推斷。又稱子樣。例如因為人力和物力所限,不能每年對全國的人口進行普查,但可以通過抽樣調查的方式來得到需要的信息。從總體中抽取樣本的過程叫抽樣。最常用的抽樣方式是簡單隨機抽樣,按這種方式抽樣,總體中每個個體都有同等的機會被抽入樣本,這樣得到的樣本稱簡單隨機樣本。樣本的平均值稱樣本均值,樣本偏離樣本均值的平方的平均值稱為樣本方差,在數理統計中,常常用樣本均值來估計總體均值,用樣本方差來估計總體方差。
均值
均值是表示一組數據集中趨勢的量數,是指在一組數據中所有數據之和再除以這組數據的個數。它是反映數據集中趨勢的一項指標。解答平均數套用題的關鍵在於確定“總數量”以及和總數量對應的總份數。在統計工作中,平均數(均值)和標準差是描述數據資料集中趨勢和離散程度的兩個最重要的測度值。
均值是統計中的一個重要概念。在統計中算術平均數常用於表示統計對象的一般水平,它是描述數據集中位置的一個統計量。既可以用它來反映一組數據的一般情況、和平均水平,也可以用它進行不同組數據的比較,以看出組與組之間的差別。用平均數表示一組數據的情況,有直觀、簡明的特點,所以在日常生活中經常用到,如平均速度、平均身高、平均產量、平均成績等等。
隨機加權
多感測器數據融合是近年來發展起來的一種數據處理新技術,對數據融合方法的研究已受到人們的普遍關注。文中首先將一種新興的隨機加權估計方法套用於多感測器數據融合,提出了一種將多源信息綜合處理的隨機加權數據融合方法。該方法依據極大似然原理,將來自不同總體(均值相同,方差不同)的隨機樣本進行有效融合,得到新的總體均值估計量,從而消除了低精度檢測結果的干擾,提高了綜合檢測結果的精度。其次,提出了一種基於隨機加權估計的多維位置數據最優融合算法。該算法用隨機加權估計對每個感測器測得的位置參數進行估計,用最優信息融合算法將這些估計進行融合,得到多感測器系統多維位置參數的最優估計。與其它融合算法相比較,隨機加權方法有許多優點如該估計值是無偏的,其估計誤差比傳統信息融合誤差小,且不需要知道參數的精確分布,易於計算。
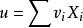 樣本均值
樣本均值 樣本均值
樣本均值 樣本均值
樣本均值式為估計總體的隨機加權數據融合,當所採用的檢測方法精度高時權值大,當所採用的檢測方法精度低時權值小,這樣便可消除低精度檢測結果的干擾,從而提高綜合檢測結果的精度。
抽樣分布
樣本均值的抽樣分布是所有的樣本均值形成的分布,即μ的機率分布。樣本均值的抽樣分布在形狀上卻是對稱的。隨著樣本量n的增大,不論原來的總體是否服從常態分配,樣本均值的抽樣分布都將趨於常態分配,其分布的數學期望為總體均值μ,方差為總體方差的1/n。這就是中心極限定理(central limit theorem)。
設總體共有N個元素,從中隨機抽取一個容量為n的樣本,在重置抽樣時,共有N·n 種抽法,即可以組成N·n不同的樣本,在不重複抽樣時,共有N·n個可能的樣本。每一個樣本都可以計算出一個均值,這些所有可能的抽樣均值形成的分布就是樣本均值的分布。但現實中不可能將所有的樣本都抽取出來,因此,樣本均值的機率分布實際上是一種理論分布。
正態總體分布
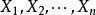 樣本均值
樣本均值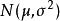 樣本均值
樣本均值 樣本均值
樣本均值設是來自正態總體的樣本,是樣本均值,則有
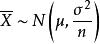 樣本均值
樣本均值