圓內接六邊形

圓內接六邊形，是指六邊形的頂點都在圓周上的六邊形叫做圓內接六邊形。

圓內接六邊形的定義與性質

定義：六邊形的頂點都在圓周上的六邊形叫做圓內接六邊形。
性質：圓內接六邊形的內角和等於720°。

圓內接正六邊形

圓內接正六邊形的定義

內接於圓的正六邊形是圓內接正六邊形。

圓內接正六邊形的性質

1、圓內接正六邊形每條邊長度相等。（即圓的六條弦長度相等）
2、圓內接正六邊形的六個內角相等，都是120°。
3、圓內接正六邊形的每條邊

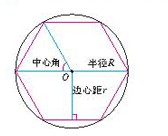圓內接正六邊形的半徑，中心角與邊心距

在圓內所對的優弧長度相等。
4、圓內接正六邊形的每條邊在圓內所對的優弧的弧度數相等。
5、圓內接正六邊形的每條邊在圓內所對的劣弧長度相等。
6、圓內接正六邊形的每條邊在圓內所對的劣弧的弧度數相等。
7、圓內接正六邊形的每條邊在圓內所對的圓心角（即每條邊的中心角）相等，都是60°。
8、圓內接正六邊形的六條半徑長度相等，都等於每條邊的長度。
9、圓內接正六邊形的邊心距等於半徑的（√3）/2倍。部分性質證明

圓內接正六邊形的每條邊在圓內所對的圓心角（即每條邊的中心角）相等，都是60°。
∵AB=BC=CD=D

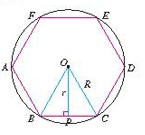證明用圖

E=EF=FA
∴∠?AOB=∠BOC=∠COD=?∠DOE=∠EOF=?∠FOA=60°圓內接正六邊形的邊心距等於半徑的（√3）/2倍。
∵OP⊥BC
∴△OPC為Rt△
∵OB=OC=BC
∴△OBC為等腰△
∵OP⊥BC
∴OP平分∠BOC
∵∠BOC=60°
∴∠POC=30°
∴∠OCP=60°
∴sin∠OCP=sin60°=OP/OC=（√3）/2
圓內接正六邊形的六條半徑長度相等，都等於每條邊的長度。
∵OB=OC
∴∠OBC=∠OCB
∵∠BOC=60°
∴?∠OBC=∠OCB=60°
∴OB=OC=BC